Jehlan

Jehlan je trojrozměrné těleso. Jeho základnu (nebo také podstavu) tvoří mnohoúhelník. Vrcholy základny jsou spojeny s jedním bodem mimo rovinu základny – tento bod se obvykle nazývá (hlavní) vrchol jehlanu.

Kolmá vzdálenost vrcholu od roviny podstavy se nazývá výška jehlanu.

Obecné vlastnosti

Objem a povrch

Objem jehlanu se vypočítá jako

${\displaystyle V={\frac {S_{p}.v}{3}}\,\!}$,

kde ${\displaystyle S_{p}\,\!}$ je obsah podstavy a ${\displaystyle v\,\!}$ výška.

Povrch jehlanu se vypočítává jako součet obsahu základny a obsahu jednotlivých trojúhelníkových stěn - jejich počet je dán počtem stran základny.

${\displaystyle S=P+Q\,}$,

kde ${\displaystyle P}$ je obsah podstavy a ${\displaystyle Q}$ je obsah pláště.

Na výše uvedených vzorcích je zajímavé, že pokud budu vrchol jehlanu posunovat v rovině rovnoběžné s rovinou základny, nemění se objem (obsah podstavy i výška zůstávají stejné), ale pouze povrch - ten může při posouvání vrcholu „dostatečně daleko“ v dané rovině růst nad všechny meze.

Souměrnost

Jehlan nemůže nikdy být středově souměrný.

Jehlan je osově souměrný pouze tehdy, je-li základna středově souměrná a průmět vrcholu jehlanu do roviny základny je shodný se středem souměrnosti základny (laičtěji: vrchol jehlanu musí ležet „kolmo nad středem souměrnosti základny“.). Osou souměrnosti je v takovém případě spojnice vrcholu se středem souměrnosti základny.

Jehlan může být rovinově souměrný pouze tehdy, je-li základna osově souměrná a průmět vrcholu jehlanu do roviny základny leží na ose souměrnosti základny. (Lidštěji: vrchol jehlanu musí ležet „kolmo nad osou souměrnosti základny“.) Rovinou souměrnosti je v takovém případě rovina určená osou souměrnosti základny a vrcholem jehlanu.

Další vlastnosti

Pokud tvoří základnu jehlanu mnohoúhelník o ${\displaystyle n\,\!}$ stranách, má jehlan:

• celkem ${\displaystyle n+1\,\!}$ vrcholů
• celkem ${\displaystyle 2\cdot n\,\!}$ hran
• celkem ${\displaystyle n+1\,\!}$ stěn

Jehlan nemá tělesové úhlopříčky, stěnové mohou být jen v základně (pro n větší než 3). Jehlan je konvexní jen tehdy, je-li konvexní jeho základna.

Speciální případy

Pokud kolmice k podstavě procházející vrcholem protíná podstavu v jejím těžišti, nazýváme takový jehlan kolmý. Pokud tomu tak není, nazýváme jej kosý.

Pokud je základnou jehlanu pravidelný mnohoúhelník a vrchol leží kolmo nad těžištěm základny, mluvíme o pravidelném jehlanu. „Pravidelnost“ jehlanu obvykle podstatně zjednodušuje výpočet jeho objemu a povrchu.

Výpočet údajů v pravidelném ${\displaystyle n}$-bokém jehlanu určeném délkou podstavné hrany ${\displaystyle a}$a jeho výškou ${\displaystyle v}$:

• Výška boční stěny:

${\displaystyle v_{s}={\frac {1}{2}}{\sqrt {4v^{2}+\left(a\cdot {\cot {\frac {\pi }{n}}}\right)^{2}}}}$

• Délka boční hrany:

${\displaystyle s={\frac {1}{2}}{\sqrt {4v^{2}+\left({\frac {a}{\sin {\frac {\pi }{n}}}}\right)^{2}}}}$

• Povrch:

${\displaystyle S={\frac {1}{4}}na^{2}\cot {\frac {\pi }{n}}\left(1+{\sqrt {1+4\left({\frac {v}{a}}\tan {\frac {\pi }{n}}\right)^{2}}}\right)}$

• Objem:

${\displaystyle V={\frac {1}{12}}na^{2}v\cdot \cot {\frac {\pi }{n}}}$

• Sklon boční hrany:

${\displaystyle \alpha =\arctan \left(2{\frac {v}{a}}\sin {\frac {\pi }{n}}\right)}$

• Sklon boční stěny:

${\displaystyle \beta =\arctan \left(2{\frac {v}{a}}\tan {\frac {\pi }{n}}\right)}$

• Odchylka bočních hran:

${\displaystyle \gamma =2\arctan {\frac {a}{\sqrt {4v^{2}+a^{2}\cot ^{2}{\frac {\pi }{n}}}}}}$

• Odchylka boční a podstavné hrany:

${\displaystyle \delta =\arctan {\sqrt {4\left({\frac {v}{a}}\right)^{2}+\cot ^{2}{\frac {\pi }{n}}}}}$

• Odchylka bočních stěn:

${\displaystyle \varepsilon =2\arcsin {\sqrt {\frac {4v^{2}\sin ^{2}{\frac {\pi }{n}}+a^{2}}{4v^{2}\tan ^{2}{\frac {\pi }{n}}+a^{2}}}}}$, speciálně pro ${\displaystyle n=4}$ je ${\displaystyle \varepsilon =2\arcsin {\sqrt {\frac {2v^{2}+a^{2}}{4v^{2}+a^{2}}}}}$

Pravidelný čtyřstěn

Pravidelný čtyřstěn je jehlan, jehož základnu i všechny tři boční stěny jsou rovnostranné trojúhelníky. Tento čtyřstěn má stejný tvar všech stěn i délku všech hran - jedná se tedy o jedno z platónských těles.

Jeho objem ${\displaystyle V\,\!}$ a obsah ${\displaystyle S\,\!}$ lze vypočítat z délky jeho hrany:

• ${\displaystyle S=a^{2}{\sqrt {3}}\,\!}$
• ${\displaystyle V={\begin{matrix}{{\sqrt {2}} \over 12}\end{matrix}}a^{3}\,\!}$

Jeho výšku lze vypočítat jako ${\displaystyle v=(a/3){\sqrt {6}}}$ .

Pravidelný čtyřboký jehlan

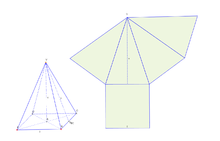
Pokud má jehlan čtvercovou základnu a vrchol kolmo nad průsečíkem úhlopříček základny, hovoříme o pravidelném čtyřbokém jehlanu.

Jeho objem ${\displaystyle V\,\!}$ a povrch ${\displaystyle S\,\!}$ lze vypočítat z délky strany základny ${\displaystyle a\,\!}$ a výšky ${\displaystyle v\,\!}$:

• ${\displaystyle V={\frac {1}{3}}a^{2}v\,\!}$
• ${\displaystyle S=a\left(a+{\sqrt {4v^{2}+a^{2}}}\right)}$

Vícerozměrná geometrická tělesa

d=2	trojúhelník	čtverec	šestiúhelník	pětiúhelník
d=3	jehlan	krychle, oktaedr	krychloktaedr, kosočtverečný dvanáctistěn	dvanáctistěn, dvacetistěn
d=4	5nadstěn	teserakt, 16nadstěn	24nadstěn	120nadstěn,600nadstěn
d=5	5simplex	penterakt, 5ortoplex
d=6	6simplex	hexerakt, 6ortoplex
d=7	7simplex	hepterakt, 7ortoplex
d=8	8simplex	okterakt, 8ortoplex
d=9	9simplex	ennerakt, 9ortoplex
d=10	10simplex	dekerakt, 10ortoplex
d=11	11simplex	hendekerakt, 11ortoplex
d=12	12simplex	dodekerakt, 12ortoplex
d=13	13simplex	triskaidekerakt, 13ortoplex
d=14	14simplex	tetradekerakt, 14ortoplex
d=15	15simplex	pentadekerakt, 15ortoplex
d=16	16simplex	hexadekerakt, 16ortoplex
d=17	17simplex	heptadekerakt, 17ortoplex
d=18	18simplex	oktadekerakt, 18ortoplex
d=19	19simplex	ennedekerakt, 19ortoplex
d=20	20simplex	ikosarakt, 20ortoplex

Literatura

• Karel Rektorys a kolektiv: Přehled užité matematiky I, Prometheus, Praha 1995, ISBN 80-85849-92-5, str. 104-106
• Marcela Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, ISBN 978-80-7358-083-4, str. 117-120

Související články

• Geometrický útvar
• Mnohostěn
• Komolý jehlan
• Válec
• Platónská tělesa

Externí odkazy

• Obrázky, zvuky či videa k tématu jehlan na Wikimedia Commons
• Slovníkové heslo jehlan ve Wikislovníku