Rhombendodekaeder

Das Rhombendodekaeder ist ein Polyeder mit zwölf rhombenförmigen Flächen, 14 Ecken und 24 Kanten. An sechs der Ecken grenzen vier Kanten und an die übrigen acht Ecken grenzen drei Kanten.

Es ist ein catalanischer Körper und dual zum Kuboktaeder. Das Rhombendodekaeder ist auch der Hüllkörper, der durch die Vereinigungsmenge der Durchdringung eines Hexaeders (Würfel) und eines Oktaeders beschrieben wird.

Wird ein Hexaeder „umgekrempelt“, entsteht ein Rhombendodekaeder. Jede Seite des Hexaeders beschreibt eine Pyramide mit dem Mittelpunkt des Hexaeders als Spitze. Diese Pyramiden werden, mit den Hexaederseiten nach innen, zusammengesetzt (also auf die Hexaederseiten aufgesetzt). Es entsteht ein Rhombendodekaeder mit dem einbeschriebenen Hexaeder als Hohlform. Daraus folgt, dass das Volumen eines Rhombendodekaeders doppelt so groß ist wie das eines Hexaeders mit der Kantenlänge der kleinen Diagonalen der Seitenflächen.

Das Rhombendodekaeder entsteht ebenfalls durch die Anwendung eines ähnlichen Vorgangs auf das Oktaeder.

Mehrere Rhombendodekaeder füllen den Raum lückenlos aus, wenn sie – wie in der nebenstehenden Grafik gezeigt – aneinandergefügt werden.

Verwandte Polyeder

• 
  Hexakisoktaeder
• 
  Deltoidalikositetraeder

Werden auf die 12 Begrenzungsflächen des Rhombendodekaeders^[1] Pyramiden mit den Flankenlängen ${\displaystyle b}$ und ${\displaystyle c\,(<b)}$ aufgesetzt, entsteht ein allgemeines Hexakisoktaeder, sofern folgende Bedingung erfüllt ist:

${\displaystyle {\tfrac {a}{3}}{\sqrt {6}}<b<{\tfrac {2}{9}}a{\sqrt {15}}}$

• Das spezielle Hexakisoktaeder mit gleichen Flächenwinkeln an den Kanten ${\displaystyle a}$ und ${\displaystyle b}$ entsteht, wenn ${\displaystyle b=2a\,({\sqrt {2}}-1)}$ ist.
• Nimmt ${\displaystyle b}$ den zuvor genannten maximalen Wert an, entartet das Hexakisoktaeder zu einem Deltoidalikositetraeder mit den Kantenlängen ${\displaystyle a}$ und ${\displaystyle b}$.

Formeln

Die folgende Tabelle enthält metrische Eigenschaften eines Rhombendodekaeders und dessen Rhomben mit einer Kantenlänge ${\displaystyle a}$ und Länge ${\displaystyle f}$ der kleinen Rhombusdiagonalen. Die Formeln werden im nächsten Abschnitt hergeleitet.

Für das Polyeder Größen eines Rhombendodekaeders Volumen ${\displaystyle V={\frac {16}{9}}\,a^{3}{\sqrt {3}}}$ Oberflächeninhalt ${\displaystyle A_{O}\,=8\,a^{2}{\sqrt {2}}}$ Inkugelradius ${\displaystyle r_{i}={\frac {a}{3}}{\sqrt {6}}}$ Umkugelradius ${\displaystyle r_{u}=f={\frac {2a}{3}}{\sqrt {3}}}$ Kantenkugelradius ${\displaystyle r_{k}={\frac {2a}{3}}{\sqrt {2}}}$ Flächenwinkel ${\displaystyle \beta =120^{\circ }}$ Flächen-Kanten-Winkel  ≈ 125° 15′ 52″ ${\displaystyle \cos \,\gamma =-{\frac {1}{3}}{\sqrt {3}}}$ 1. Eckenraumwinkel  (3 Flächen) ${\displaystyle \Omega _{3}=\pi }$ 2. Eckenraumwinkel   (4 Flächen) ${\displaystyle \Omega _{4}={\frac {2}{3}}\pi }$ Sphärizität  ≈ 0,9047 ${\displaystyle \Psi ={\frac {\sqrt[{3}]{18\,\pi }}{3{\sqrt {2}}}}}$

Für die Rhomben Größen der Rhomben Flächeninhalt ${\displaystyle A={\frac {2}{3}}a^{2}{\sqrt {2}}}$ Inkreisradius ${\displaystyle \rho ={\frac {a}{3}}{\sqrt {2}}}$ Lange Diagonale ${\displaystyle e={\frac {2}{3}}a{\sqrt {6}}=f{\sqrt {2}}}$ Kurze Diagonale ${\displaystyle f={\frac {2}{3}}a{\sqrt {3}}}$ Spitze Winkel (2) ≈ 70° 31′ 44″ ${\displaystyle \cos \,\delta _{1}={\frac {1}{3}}}$ Stumpfe Winkel (2) ≈ 109° 28′ 16″ ${\displaystyle \cos \,\delta _{2}=-{\frac {1}{3}}}$

Herleitung der Formeln

Einbeschriebener Würfel

Ein Rhombendodekaeder kann man sich aus einem Würfel (Kantenlänge ${\displaystyle f}$) und auf den 6 Seitenflächen errichteten quadratischen Pyramiden entstanden denken (siehe Bild). Da je zwei Pyramiden-Dreiecke, die eine Würfelkante gemeinsam haben, einen Rhombus bilden müssen, gilt für die Pyramidenhöhe ${\displaystyle h={\tfrac {f}{2}}}$. Die kurze Diagonale eines Rhombus hat die Länge ${\displaystyle f}$, die lange Diagonale hat die Länge ${\displaystyle e=f{\sqrt {2}}}$.

Die Kantenlänge ${\displaystyle a}$ des Rhombendodekaeders ist gleich der Länge einer Rhombusseite (siehe unteres Bild)

${\displaystyle a={\sqrt {(e/2)^{2}+(f/2)^{2}}}={\frac {\sqrt {3}}{2}}f\ }$ und

${\displaystyle f={\frac {2a}{3}}{\sqrt {3}},\quad e={\frac {2a}{3}}{\sqrt {6}}}$.

Oberfläche und Volumen

Die Oberfläche ist gleich 12 mal der Fläche eines Rhombus.

${\displaystyle A_{O}=12\cdot {\frac {e\cdot f}{2}}=8{\sqrt {2}}\;a^{2}\ .}$

Das Volumen des Rhombendodekaeders ist gleich dem Volumen des Würfels plus 6 mal dem Volumen einer Pyramide. Da eine Pyramide halb so hoch ist wie der Würfel, füllen die Pyramiden nach Drehen der Spitzen nach innen den Würfel voll aus. Das Volumen des Rhombendodekaeders ist also

${\displaystyle V=2f^{3}={\frac {16}{9}}{\sqrt {3}}\;a^{3}}$.

Um-, In- und Kanten-Kugelradien

Die Umkugel geht durch die Spitzen der Pyramiden und hat den Radius

${\displaystyle \ r_{u}=f={\frac {2a}{3}}{\sqrt {3}}}$.

Die Umkugel enthält aber nicht die Würfelpunkte des Rhombendodekaeders!

Die Inkugel berührt die Rhomben und hat den Radius (siehe Bild)

${\displaystyle \ r_{i}={\frac {e}{2}}={\frac {f}{2}}{\sqrt {2}}={\frac {a}{3}}{\sqrt {6}}}$.

Für den Kantenkugel-Radius und den Winkel zwischen einer Kante und einem Rhombus ist der in dem unteren Bild eingezeichnete Steigungswinkel ${\displaystyle \varphi }$ einer Pyramidenkante wesentlich. Für ihn gilt:

${\displaystyle \cos \varphi ={\tfrac {e/2}{a}}={\sqrt {\tfrac {2}{3}}}\to \varphi \approx 35{,}26^{\circ }}$.

Damit folgt für den Kantenkugelradius

${\displaystyle r_{k}=f\cos \varphi ={\sqrt {\tfrac {2}{3}}}f={\frac {2}{3}}{\sqrt {2}}a\ }$.

Der Inkreisradius eines Rhombus ist

${\displaystyle \rho ={\frac {f}{2}}\cos \varphi ={\frac {a}{3}}{\sqrt {3}}}$.

Winkel

Der Winkel zwischen Kante und Rhombus ist (siehe Bild)

${\displaystyle \gamma =90^{\circ }+\varphi \approx 125{,}26^{\circ }}$.

Es gilt: ${\displaystyle \ \cos \gamma =-\sin \varphi =-{\frac {1}{3}}{\sqrt {3}}}$.

Der Winkel zwischen zwei Rhomben ist gleich dem Winkel zwischen zwei Dreiecken einer Pyramide. Entweder man berechnet den Winkel mit Hilfe der Flächennormalen oder verwendet die Formel aus dem Artikel über Pyramiden. Es ergibt sich

${\displaystyle \beta =120^{\circ }}$.

Die Winkel in einem Rhombus sind (siehe unteres Bild)

kleiner Winkel: ${\displaystyle \ \delta _{1}=2\varphi \approx 70{,}53^{\circ }}$.

großer Winkel: ${\displaystyle \ \delta _{2}=180^{\circ }-\delta _{1}\approx 109{,}47^{\circ }}$.

Da 6 umgedrehte Pyramiden den Raum des Würfels voll ausfüllen, ist der Raumwinkel in einer Pyramidenspitze 1/6 des vollen Raumwinkels:

${\displaystyle \Omega _{4}={\frac {1}{6}}\cdot 4\pi ={\frac {2}{3}}\pi }$.

Für den Raumwinkel in einem Punkt mit 3 Kanten (Würfelpunkt) ergibt sich aus der Ebenen-Formel im Artikel Raumwinkel

${\displaystyle \Omega _{3}=3\beta -\pi =\pi }$.

Parkettierung

Zerlegt man den Raum so in gleich große rote und grüne Würfel, dass jeder rote Würfel nur von grünen Würfeln und umgekehrt umgeben ist, zerlegt jeden grünen Würfel in 6 Pyramiden mit dem Mittelpunkt als Spitze, klebt jede Pyramide an den benachbarten roten Würfel, mit dem sie ein Quadrat gemeinsam hat, so entstehen Rhombendodekaeder, die den Raum überdecken.

Das Bild zeigt eine Parkettierung des Raumes mit Rhombendodekaedern. Zwei benachbarte Polyeder haben entweder einen Rhombus gemeinsam oder nur einen Punkt (Kegelspitze). Die einbeschriebenen Würfel sind dunkelrot. In einer Pyramidenspitze treffen 6 Polyeder zusammen, in einer Würfelecke sind es 4.

Vorkommen

• In der Natur kommt das Rhombendodekaeder als typische Kristallform bei Mineralen der Granatgruppe vor und wird daher auch Granatoeder genannt. Es kann als spezielle Form {110} in allen kubischen Kristallklassen auftreten.
• Die erste Brillouin-Zone des kubisch innenzentrierten Gitters hat die Form eines Rhombendodekaeders.
• Das Rhombendodekaeder ist eine dreidimensionale Projektion eines vierdimensionalen Würfels (Tesserakt).

• 
  Andradit-Einkristall als Vertreter der Granatgruppe
• 
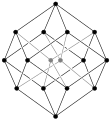  Parallelprojektion eines Tesserakts

Anmerkungen

1. ↑ Kantenlänge a

Literatur

• Susanne Müller-Philipp, Hans-Joachim Gorski: Leitfaden Geometrie: Für Studierende der Lehrämter. Springer-Verlag, 2009, ISBN 978-3-8348-9230-0, S. 47.

Weblinks

• Eric W. Weisstein: Rhombendodekaeder. In: MathWorld (englisch).
• Mineralienatlas:Rhombendodekaeder Interaktive Darstellung des Rhombendodekaeders im Mineralienatlas