Satz des Thales

Der Satz des Thales ist ein Satz der Geometrie und ein Spezialfall des Kreiswinkelsatzes. Vereinfacht lautet er: Alle von einem Halbkreis umschriebenen Dreiecke sind rechtwinklig.

Der erste Beweis wird dem antiken griechischen Mathematiker und Philosophen Thales von Milet zugeschrieben.^[1] Die Aussage des Satzes war bereits vorher in Ägypten und Babylonien bekannt.

Formulierung des Satzes und seiner Umkehrung

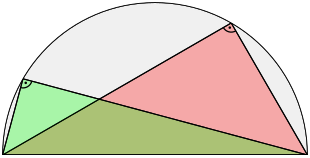
Exakte Formulierung: Konstruiert man ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis) und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.

Oder: Liegt der Punkt ${\displaystyle C}$ eines Dreiecks ${\displaystyle ABC}$ auf einem Halbkreis über der Strecke ${\displaystyle {\overline {AB}}}$, dann hat das Dreieck bei ${\displaystyle C}$ immer einen rechten Winkel.

Auch die Umkehrung des Satzes ist korrekt: Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse, also der längsten Seite des Dreiecks, die dem rechten Winkel gegenüberliegt.

Oder: Hat das Dreieck ${\displaystyle ABC}$ bei ${\displaystyle C}$ einen rechten Winkel, so liegt ${\displaystyle C}$ auf einem Kreis mit der Hypotenuse ${\displaystyle {\overline {AB}}}$ als Durchmesser.

Beweise

Euklid leitet den Satz des Thales im dritten Band seiner Elemente mit Hilfe folgender Sätze, die ebenfalls Thales zugeschrieben werden und im ersten Band enthalten sind, her:^[2]

Beweis mit gleichschenkligen Dreiecken

• In jedem gleichschenkligen Dreieck sind die Winkel an der Basis gleich.^[3]
• Die Innenwinkelsumme im Dreieck ist 180°.

ABC sei ein Dreieck innerhalb eines Kreises mit ${\displaystyle {\overline {AB}}}$ als Kreisdurchmesser und dem Radius ${\displaystyle r}$. Dann ist der Mittelpunkt M der Strecke ${\displaystyle {\overline {AB}}}$ auch der Kreismittelpunkt. Die Streckenlängen ${\displaystyle {\overline {AM}}}$, ${\displaystyle {\overline {BM}}}$ und ${\displaystyle {\overline {CM}}}$ sind also gleich dem Radius ${\displaystyle r}$.

Die Strecke ${\displaystyle {\overline {CM}}}$ teilt das Dreieck ${\displaystyle ABC}$ in zwei Dreiecke ${\displaystyle AMC}$ und ${\displaystyle BCM}$ auf, die gleichschenklig sind. Die Basiswinkel dieser Dreiecke, also die Winkel an der Grundseite ${\displaystyle {\overline {AC}}}$ bzw. ${\displaystyle {\overline {BC}}}$, sind daher jeweils gleich (${\displaystyle \alpha }$ beziehungsweise ${\displaystyle \beta }$ in der Abbildung).

Die Winkelsumme im Dreieck ${\displaystyle ABC}$ beträgt 180°:

${\displaystyle \alpha +\beta +\alpha +\beta =180^{\circ }}$

${\displaystyle 2\cdot (\alpha +\beta )=180^{\circ }}$

Dividiert man diese Gleichung auf beiden Seiten durch 2, so ergibt sich

${\displaystyle \alpha +\beta \,=\,90^{\circ }}$.

Damit ist gezeigt, dass der Winkel ${\displaystyle \alpha +\beta }$  mit Scheitel ${\displaystyle C}$ ein rechter Winkel ist.

Die Umkehrung des Satzes von Thales lässt sich auf die Aussage zurückführen, dass die Diagonalen eines Rechtecks gleich lang sind und sich gegenseitig halbieren.

Beweis mit Vervollständigung zum Rechteck

Wird der Punkt ${\displaystyle C}$ am Durchmesser ${\displaystyle {\overline {AB}}}$ und anschließend an der Mittelsenkrechten von ${\displaystyle {\overline {AB}}}$ gespiegelt, dann liegt der Bildpunkt ${\displaystyle D}$ wegen Symmetrie auf dem unteren Halbkreis über der Seite ${\displaystyle {\overline {AB}}}$. Das ist eine Punktspiegelung am Kreismittelpunkt ${\displaystyle M}$. Daher sind die Seiten und ${\displaystyle {\overline {AC}}}$ und ${\displaystyle {\overline {BD}}}$ sowie ${\displaystyle {\overline {AD}}}$ und ${\displaystyle {\overline {BC}}}$ parallel und das Viereck ${\displaystyle ACBD}$ ist ein Parallelogramm. Weil die Diagonalen ${\displaystyle {\overline {AB}}}$ und ${\displaystyle {\overline {CD}}}$ Durchmesser des Kreises und daher gleich lang sind, ist das Parallelogramm ein Rechteck und der Winkel bei ${\displaystyle C}$ ein rechter Winkel.

Beweis mit kartesischen Koordinaten

Der Kreismittelpunkt sei der Koordinatenursprung. Sind der Radius ${\displaystyle r}$ und die Punkte ${\displaystyle A=(-r,0)}$, ${\displaystyle B=(r,0)}$ und ${\displaystyle C=(x,y)}$ mit kartesischen Koordinaten gegeben, dann gilt nach dem Satz des Pythagoras ${\displaystyle x^{2}+y^{2}=r^{2}}$. Wegen ${\displaystyle (r+x)^{2}+y^{2}={\overline {AC}}^{2}}$ und ${\displaystyle (r-x)^{2}+y^{2}={\overline {BC}}^{2}}$ gilt im Dreieck ${\displaystyle ABC}$ die Gleichung

${\displaystyle {\overline {AC}}^{2}+{\overline {BC}}^{2}=((r+x)^{2}+y^{2})+((r-x)^{2}+y^{2})=2r^{2}+2(x^{2}+y^{2})=4r^{2}={\overline {AB}}^{2}}$.

Aus der Umkehrung des Satzes des Pythagoras folgt, dass das Dreieck ${\displaystyle ABC}$ im Punkt ${\displaystyle C}$ rechtwinklig ist.

Mit dem Satz des Pythagoras kann auch gezeigt werden, dass das Skalarprodukt der Vektoren ${\displaystyle {\vec {AC}}}$ und ${\displaystyle {\vec {CB}}}$ gleich Null ist:

Es ist ${\displaystyle {\vec {AC}}={\binom {x_{C}}{y_{C}}}\ominus {\binom {-r}{0}}={\binom {r+x_{C}}{y_{C}}}}$ und ${\displaystyle {\vec {CB}}={\binom {r}{0}}\ominus {\binom {x_{C}}{y_{C}}}={\binom {r-x_{C}}{-y_{C}}}}$.

${\displaystyle {\vec {AC}}\odot {\vec {CB}}=(r+x_{C})\cdot (r-x_{C})-{y_{C}}^{2}=r^{2}-{x_{C}}^{2}-{y_{C}}^{2}\ {\stackrel {\text{Satz des Pythagoras}}{=}}\ 0={\overline {AC}}\cdot {\overline {CB}}\cdot \cos(\measuredangle ACB)}$,

woraus folgt, dass der Kosinus des Winkels im Punkt C gleich Null ist und somit das Dreieck ABC einen rechten Winkel in C hat.

Trigonometrischer Beweis

Sind der Winkel ${\displaystyle \beta }$, der Radius ${\displaystyle r}$ und die Punkte ${\displaystyle A=(-r,0)}$, ${\displaystyle B=(r,0)}$ mit kartesischen Koordinaten gegeben, dann hat der Punkt ${\displaystyle C}$ die Koordinaten ${\displaystyle C=(r\cdot \cos(\beta ),r\cdot \sin(\beta ))}$. Die Seite ${\displaystyle {\overline {AC}}}$ hat die Steigung

${\displaystyle {\frac {r\cdot \sin(\beta )-0}{r\cdot \cos(\beta )-(-r)}}={\frac {\sin(\beta )}{\cos(\beta )+1}}}$

und die Seite ${\displaystyle {\overline {BC}}}$ hat die Steigung

${\displaystyle {\frac {r\cdot \sin(\beta )-0}{r\cdot \cos(\beta )-r}}={\frac {\sin(\beta )}{\cos(\beta )-1}}}$.

Wegen ${\displaystyle \sin ^{2}(\beta )+\cos ^{2}(\beta )=1}$ ist das Produkt der Steigungen gleich

${\displaystyle {\frac {\sin(\beta )}{\cos(\beta )+1}}\cdot {\frac {\sin(\beta )}{\cos(\beta )-1}}={\frac {\sin ^{2}(\beta )}{\cos ^{2}(\beta )-1}}={\frac {\sin ^{2}(\beta )}{-\sin ^{2}(\beta )}}=-1}$.

Daraus folgt, dass die Seiten ${\displaystyle {\overline {AC}}}$ und ${\displaystyle {\overline {BC}}}$ zueinander orthogonal sind und einen rechten Winkel bilden.

Einen weiteren Beweis findet man hier: Wikibooks: Beweisarchiv.

Anwendungen

Konstruktion einer Kreistangente

Eine wichtige Anwendung des Satzes von Thales ist u. a. die Konstruktion der beiden Tangenten an einen Kreis k durch einen außerhalb dieses Kreises gelegenen Punkt ${\displaystyle P}$.

Gegeben sei der Radius ${\displaystyle r}$ vom Kreis ${\displaystyle k}$ mit seinem Mittelpunkt ${\displaystyle O}$ sowie der Abstand des Punktes ${\displaystyle P}$ von ${\displaystyle O}$. Vom Punkt ${\displaystyle T}$ wissen wir nur, dass er auf der Kreislinie, irgendwo im ersten Viertel vom Kreis ${\displaystyle k}$, liegen muss. Würde man nur diese Bedingung berücksichtigen, könnte man unendlich viele Dreiecke ${\displaystyle OPT}$ einzeichnen.

Da die obere durch ${\displaystyle P}$ verlaufende Tangente ${\displaystyle t}$ den Kreis ${\displaystyle k}$ genau im Punkt ${\displaystyle T}$ berührt, muss das Dreieck ${\displaystyle OPT}$ einen rechten Winkel am Punkt ${\displaystyle T}$ haben (Grundeigenschaft der Kreistangente), oder anders formuliert: Die Strecke ${\displaystyle {\overline {OT}}}$ muss senkrecht auf der Tangente ${\displaystyle t}$ stehen.

Um ein Dreieck ${\displaystyle OPT}$ zu finden, das auch rechtwinklig ist, ermitteln wir von der Strecke ${\displaystyle {\overline {OP}}}$ den Mittelpunkt ${\displaystyle H}$ mithilfe der Mittelsenkrechten, zeichnen einen Kreis mit dem Radius ${\displaystyle {\overline {HO}}}$ um den Mittelpunkt ${\displaystyle H}$ und machen uns das Prinzip des Thaleskreises zunutze: Alle Dreiecke mit der Grundseite ${\displaystyle {\overline {OP}}}$, deren dritter Eckpunkt auf dem Thaleskreis liegt, sind rechtwinklig. Dies gilt natürlich auch für das Dreieck ${\displaystyle OPT}$.

Der Berührpunkt ${\displaystyle T}$ kann deshalb nur der Schnittpunkt des Kreises ${\displaystyle k}$ mit dem hellgrauen Kreis sein. Durch Verbinden von ${\displaystyle P}$ mit ${\displaystyle T}$ erhält man nun die gesuchte Tangente ${\displaystyle t}$ (in der Zeichnung rot).

Es existiert eine zweite, symmetrische Lösung in der unteren Hälfte des Kreises. Die Tangente ${\displaystyle t'}$ (ebenfalls rot gezeichnet) berührt den Kreis ebenfalls, und zwar im Punkt ${\displaystyle T'}$.

Quadratur des Rechtecks

Eine weitere Anwendung ist die Quadratur des Rechtecks.

Konstruktion reeller Quadratwurzeln

Mithilfe des Satzes des Thales lassen sich die folgenden Quadratwurzeln konstruieren:^[4]

• ${\displaystyle {\sqrt {q}}}$ aus ${\displaystyle q>0}$ und ${\displaystyle {\sqrt {c}}}$ aus ${\displaystyle c>1}$ (siehe Zahl größer als 1).
• ${\displaystyle {\sqrt {p\cdot q}}}$ aus ${\displaystyle c=1,\;{\sqrt {q}}}$ aus ${\displaystyle q<1}$ und ${\displaystyle {\sqrt {p}}}$ aus ${\displaystyle p<1}$ (siehe Zahl kleiner als 1).

Zahl größer als 1

Soll die Quadratwurzel einer reellen Zahl, die größer als 1 ist, gefunden werden, ohne vorherige Aufteilung der Zahl in ${\displaystyle p}$- und ${\displaystyle q}$-Anteile, eignet sich dafür die Methode, die das nebenstehende Bild zeigt. Im Prinzip sind damit auch Quadratwurzeln von Zahlen, die kleiner als 1 sind, vorstellbar.

Es beginnt mit dem Einzeichnen der Strecke ${\displaystyle {\overline {BD}}}$ mit Länge ${\displaystyle p=1}$ auf einer hier nicht näher bezeichneten Geraden. Ist die gegebene Zahl ${\displaystyle q}$ eine ganze Zahl, wird das Produkt ${\displaystyle q\cdot {\overline {BD}}}$ ab dem Punkt ${\displaystyle D}$ auf die Gerade abgetragen; d. h. ist z. B. die Zahl ${\displaystyle q=8}$, wird die Strecke ${\displaystyle {\overline {BD}}}$ achtmal abgetragen. Der dadurch entstehende Schnittpunkt ${\displaystyle A}$ bringt die Hypotenuse ${\displaystyle c=p+q}$ des entstehenden Dreiecks ${\displaystyle ABC}$.

Ist ${\displaystyle q}$ eine reelle Zahl, besteht u. a. auch die Möglichkeit, ${\displaystyle q}$ mithilfe des dritten Strahlensatzes zu konstruieren.

Es folgen die Senkrechte auf ${\displaystyle c}$ im Punkt ${\displaystyle D}$ und die Halbierung der Seite ${\displaystyle c}$ in ${\displaystyle M}$. Abschließend wird der Thaleskreis um ${\displaystyle M}$ gezogen.

• Nach dem Höhensatz des Euklid gilt ${\displaystyle h^{2}=p\cdot q}$, daraus folgt ${\displaystyle h^{2}=1\cdot q}$,

somit ist die Höhe des rechtwinkligen Dreiecks ${\displaystyle ABC}$ gleich der Quadratwurzel aus ${\displaystyle q}$.

• Nach dem Kathetensatz des Euklid gilt ${\displaystyle a^{2}=p\cdot c,}$ daraus folgt ${\displaystyle a^{2}=1\cdot c,}$

somit ist die Seitenlänge ${\displaystyle a}$ des rechtwinkligen Dreiecks ${\displaystyle ABC}$ gleich der Quadratwurzel aus ${\displaystyle c}$.

Zahl kleiner als 1

Ist die Quadratwurzel einer Zahl, die kleiner als ${\displaystyle 1}$ ist, gesucht, eignet sich dafür die Methode, die das nebenstehende Bild zeigt.

Es beginnt ab dem Punkt ${\displaystyle A}$ (Wert ${\displaystyle 0}$) mit einer Halbgeraden. Darauf wird die Strecke ${\displaystyle {\overline {AB}}}$ mit Länge ${\displaystyle 1}$ und die Strecke ${\displaystyle {\overline {AE}}}$ mit Länge ${\displaystyle 0{,}1}$ bestimmt. Dabei ergibt sich die Hypotenuse ${\displaystyle c}$ des entstehenden Dreiecks ${\displaystyle ABC.}$ Hat die gegebene Dezimalzahl ${\displaystyle q}$ nur eine Nachkommastelle, wird das Produkt ${\displaystyle q\cdot {\overline {AE}}}$ ab dem Punkt ${\displaystyle A}$ abgetragen; d. h. ist z. B. ${\displaystyle q=0{,}8}$ wird die Strecke ${\displaystyle {\overline {AE}}}$ achtmal abgetragen. Der dadurch entstehende Schnittpunkt ${\displaystyle D}$ bringt ${\displaystyle c=p+q.}$

Wenn die gegebene Dezimalzahl ${\displaystyle q}$ mehr als eine Nachkommastelle hat, z. B. ${\displaystyle q=0{,}86}$, besteht u. a. die Möglichkeit, wie bereits oben im Abschnitt Zahl größer als 1 darauf hingewiesen, ${\displaystyle q}$ mithilfe des dritten Strahlensatzes zu konstruieren.

Es folgen die Senkrechte auf die Strecke ${\displaystyle {\overline {AB}}}$ im Punkt ${\displaystyle D}$ und die Halbierung der Seite ${\displaystyle c}$ in ${\displaystyle M.}$ Abschließend wird der Thaleskreis (Radius ${\displaystyle =0{,}5}$) um ${\displaystyle M}$ gezogen.

• Nach dem Höhensatz des Euklid gilt ${\displaystyle h^{2}=p\cdot q,}$

somit ist die Höhe ${\displaystyle h}$ des rechtwinkligen Dreiecks ${\displaystyle ABC}$ gleich der Quadratwurzel aus ${\displaystyle p\cdot q}$.

Wegen ${\displaystyle h={\sqrt {p\cdot q}}}$ gilt auch:

Im rechtwinkligen Dreieck ${\displaystyle ABC}$ ist die Länge ${\displaystyle h}$ das geometrische Mittel der Längen ${\displaystyle p}$ und ${\displaystyle q}$.

• Nach dem Satz des Pythagoras gilt für die Seitenlänge ${\displaystyle b}$:

${\displaystyle b^{2}=q^{2}+p\cdot q}$, darin ist ${\displaystyle p=1-q}$, damit ergibt sich

${\displaystyle b^{2}=q^{2}+q\cdot \left(1-q\right)}$

${\displaystyle b^{2}=q^{2}+q-q^{2}\Rightarrow }$

${\displaystyle b={\sqrt {q}},}$

somit ist die Seitenlänge ${\displaystyle b}$ des rechtwinkligen Dreiecks ${\displaystyle ABC}$ gleich der Quadratwurzel aus ${\displaystyle q}$.

Für die Seitenlänge ${\displaystyle a:}$

Mit den entsprechenden Werten für die Seitenlänge ${\displaystyle a}$ ergibt sich

${\displaystyle a={\sqrt {p}},}$

somit ist die Seitenlänge ${\displaystyle a}$ des rechtwinkligen Dreiecks ${\displaystyle ABC}$ gleich der Quadratwurzel aus ${\displaystyle p.}$

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie. 3., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2007, ISBN 978-3-540-49327-3.
• Hans Schupp: Elementargeometrie (= Uni-Taschenbücher 669). Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 41.

Weblinks

• Euklids Beweis (Satz III.31). (PDF; 530 kB) Deutsch von Rudolf Haller.
• Animierte, interaktive Grafik zum Verständnis. Walter Fendt

Einzelnachweise

1. ↑ Diogenes Laertius: Leben und Meinungen berühmter Philosophen. Erster Band, Buch I−VI. Verlag von Felix Meiner, Leipzig 1921, S. 12, Ziffer 24; Textarchiv – Internet Archive
2. ↑ Thomas Heath: A History of Greek Mathematics. Band 1: From Thales to Euclid. Dover Publications, New York 1981, ISBN 0-486-24073-8.
3. ↑ Proklos. In: Euklid: Die Elemente. I,250,20
4. ↑ Klaus Pommerening: Konstruierbarkeit mit Zirkel und Lineal – ein Vorspiel zur Galois-Theorien. (PDF) Quadratwurzel aus einer Strecke (H ̈ohensatz). Universität Mainz, April 2020, S. 8, abgerufen am 23. Januar 2023.