Schriftliche Multiplikation

Schriftliche Multiplikation ist ein Rechenverfahren (Algorithmus), mithilfe dessen eine Multiplikation zweier mehrstelliger Zahlen durch eine schriftliche Darstellung ausgeführt werden kann. Im Folgenden wird das Verfahren für natürliche Zahlen beschrieben. Die Erweiterung auf reelle Zahlen mit endlicher Anzahl an Dezimalstellen erfolgt anschließend.

Verfahren

Das allgemein übliche Verfahren besteht darin, die Multiplikation einer mehrstelligen Zahl (Multiplikand) mit einer zweiten mehrstelligen Zahl (Multiplikator) in mehrere Multiplikationen der ersten Zahl mit einer einstelligen Zahl aufzuteilen, indem man die zweite Zahl in ihre Ziffern zerlegt. Dann muss man diese Ergebnisse mit dem Stellenwert der jeweiligen Ziffer des Multiplikators durch Ergänzen der erforderlichen Anzahl an Nullen multiplizieren und am Schluss alles addieren. Die dabei verwendete Schreibweise wird im unten angeführten Beispiel dargestellt.

Mathematischer Hintergrund

Eine natürliche ${\displaystyle n}$-stellige Dezimalzahl ${\displaystyle a}$ mit der Ziffernfolge

${\displaystyle a_{n-1}a_{n-2}\dotsb a_{1}a_{0}}$

lässt sich als Summe einstelliger Vielfacher von Zehnerpotenzen darstellen:

${\displaystyle a_{n-1}a_{n-2}\dotsb a_{1}a_{0}=a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0}}$

${\displaystyle a=\sum _{i=0}^{n-1}a_{i}\cdot 10^{i}}$

Die Multiplikation einer ${\displaystyle n}$-stelligen Zahl ${\displaystyle a}$ mit einer ${\displaystyle m}$-stelligen Zahl ${\displaystyle b}$ entspricht also der Multiplikation

${\displaystyle (a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0})\cdot (b_{m-1}\cdot 10^{m-1}+b_{m-2}\cdot 10^{m-2}+\dotsb +b_{1}\cdot 10^{1}+b_{0}\cdot 10^{0})}$

${\displaystyle a\cdot b=\left(\sum _{i=0}^{n-1}a_{i}\cdot 10^{i}\right)\cdot \left(\sum _{j=0}^{m-1}b_{j}\cdot 10^{j}\right)}$

Fasst man die Produkte der Ziffern mit ihrem Stellenwert als Elemente zweier Vektoren auf, so kann man die Multiplikation als Summe der Elemente des dyadischen Produkts der Vektoren zu einer Matrix auffassen:

${\displaystyle {\begin{pmatrix}a_{n-1}\cdot 10^{n-1}\\a_{n-2}\cdot 10^{n-2}\\\vdots \\a_{1}\cdot 10^{1}\\a_{0}\cdot 10^{0}\end{pmatrix}}\otimes {\begin{pmatrix}b_{m-1}\cdot 10^{m-1}\\b_{m-2}\cdot 10^{m-2}\\\vdots \\b_{1}\cdot 10^{1}\\b_{0}\cdot 10^{0}\end{pmatrix}}={\begin{pmatrix}{a_{n-1}b_{m-1}\cdot 10^{n+m-2}}&{a_{n-1}b_{m-2}\cdot 10^{n+m-3}}&\dotsb &{a_{n-1}b_{1}\cdot 10^{n}}&{a_{n-1}b_{0}\cdot 10^{n-1}}\\a_{n-2}b_{m-1}\cdot 10^{n+m-3}&a_{n-2}b_{m-2}\cdot 10^{n+m-4}&\dotsb &a_{n-2}b_{1}\cdot 10^{n-1}&a_{n-2}b_{0}\cdot 10^{n-2}\\\vdots &\vdots &\dotsb &\vdots &\vdots \\a_{1}b_{m-1}\cdot 10^{m}&a_{1}b_{m-2}\cdot 10^{m-1}&\dotsb &a_{1}b_{1}\cdot 10^{2}&a_{1}b_{0}\cdot 10^{1}\\a_{0}b_{m-1}\cdot 10^{m-1}&a_{0}b_{m-2}\cdot 10^{m-2}&\dotsb &a_{0}b_{1}\cdot 10^{1}&a_{0}b_{0}\cdot 10^{0}\end{pmatrix}}}$

Beim o. g. Verfahren werden alle Matrixelemente errechnet und dabei auch spaltenweise addiert. Diese Spaltensummen werden notiert und dann schriftlich addiert, sodass man das Gesamtergebnis erhält.

Die Ergebnisse der Spalten sind:

${\displaystyle (a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0})\cdot (b_{m-1}\cdot 10^{m-1})}$

${\displaystyle (a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0})\cdot (b_{m-2}\cdot 10^{m-2})}$

${\displaystyle \dotsb }$

${\displaystyle (a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0})\cdot (b_{1}\cdot 10^{1})}$

${\displaystyle (a_{n-1}\cdot 10^{n-1}+a_{n-2}\cdot 10^{n-2}+\dotsb +a_{1}\cdot 10^{1}+a_{0}\cdot 10^{0})\cdot (b_{0}\cdot 10^{0})}$

Beispiel

Als Beispiel nehmen wir die Zahlen ${\displaystyle a=8642}$ und ${\displaystyle b=9731}$. Dann ergeben sich die Teilschritte

${\displaystyle (8\cdot 10^{3}+6\cdot 10^{2}+4\cdot 10^{1}+2\cdot 10^{0})\cdot (9\cdot 10^{3})}$

${\displaystyle (8\cdot 10^{3}+6\cdot 10^{2}+4\cdot 10^{1}+2\cdot 10^{0})\cdot (7\cdot 10^{2})}$

${\displaystyle (8\cdot 10^{3}+6\cdot 10^{2}+4\cdot 10^{1}+2\cdot 10^{0})\cdot (3\cdot 10^{1})}$

${\displaystyle (8\cdot 10^{3}+6\cdot 10^{2}+4\cdot 10^{1}+2\cdot 10^{0})\cdot (1\cdot 10^{0})}$

also

${\displaystyle (8000+600+40+2)\cdot 9000}$

${\displaystyle (8000+600+40+2)\cdot 700}$

${\displaystyle (8000+600+40+2)\cdot 30}$

${\displaystyle (8000+600+40+2)\cdot 1}$

Mit Hilfe einer versetzten Platzierung der Werte auf bevorzugt kariertem Papier kann man das Notieren der Zehnerpotenzen (in den Grafiken rot dargestellt) einsparen. Unter Verwendung des kleinen Einmaleins und Addition erhält man für die Zeilen:

Das ganze Schema mit verkürzter Notation der Zeilen ist dann:

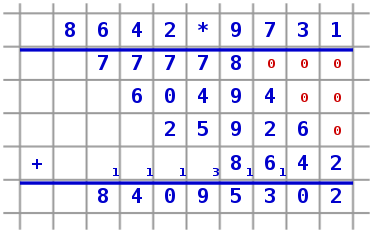
Damit ist die Multiplikation vollständig durchgeführt.

Dezimalstellen und Vorzeichen

Hat mindestens ein Faktor Nachkommastellen, so wird die Multiplikation zunächst so durchgeführt, als ob es ganze Zahlen wären. Danach muss man das Komma so setzen, dass die Anzahl der Nachkommastellen des Ergebnisses der Summe der Anzahl an Nachkommastellen der Faktoren entspricht.

Hat mindestens ein Faktor ein negatives Vorzeichen, so multipliziert man zuerst die Beträge und bestimmt danach das Vorzeichen mit Hilfe der Vorzeichenregeln.

Siehe auch

• Russische Bauernmultiplikation
• Duplation

Literatur

• Friedhelm Padberg, Andreas Büchter: Einführung Mathematik Primarstufe – Arithmetik. 2. Auflage. Springer, 2015, ISBN 978-3-662-43449-9, S. 50–55.
• Petra Knöß: Fundamentale Ideen der Informatik im Mathematikunterricht: Grundsätzliche Überlegungen und Beispiele für die Primarstufe. Springer, 1989, S. 189–201.
• Schülerduden – Mathematik I. 8. Auflage. Duden-Verlag, 2008, ISBN 978-3-411-04208-1, S. 198, 202, 412–414.

Weblinks

• Anleitung Schriftliches Multiplizieren (Lehrerfortbildung Baden-Württemberg)
• Schriftliche Rechenverfahren international (Universität Duisburg-Essen)