Small snub icosicosidodecahedron

Geometric figure
Small snub icosicosidodecahedron
Type Uniform star polyhedron
Elements F = 112, E = 180
V = 60 (χ = −8)
Faces by sides (40+60){3}+12{5/2}
Coxeter diagram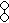
Wythoff symbol | 5/2 3 3
Symmetry group Ih, [5,3], *532
Index references U32, C41, W110
Dual polyhedron Small hexagonal hexecontahedron
Vertex figure
35.5/2
Bowers acronym Seside
3D model of a small snub icosicosidodecahedron

In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, ß{3,5}.

The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.

Convex hull

Its convex hull is a nonuniform truncated icosahedron.


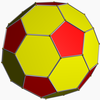Truncated icosahedron
(regular faces)
Convex hull
(isogonal hexagons)
Small snub icosicosidodecahedron

Cartesian coordinates

Cartesian coordinates for the vertices of a small snub icosicosidodecahedron are all the even permutations of

( ± [ 1 − φ + α ] ,       0 , ± [ 3 + φ α ] ) ( ± [ φ − 1 + α ] , ± 2 , ± [ 2 φ − 1 + φ α ] ) ( ± [ φ + 1 + α ] , ± 2 [ φ − 1 ] , ± [ 1 + φ α ] ) {\displaystyle {\begin{array}{clllc}{\Bigl (}&\pm {\bigl [}1-\varphi +\alpha {\bigr ]},&\ \ \ \,0,&\pm {\bigl [}3+\varphi \alpha {\bigr ]}&{\Bigr )}\\{\Bigl (}&\pm {\bigl [}\varphi -1+\alpha {\bigr ]},&\pm \,2,&\pm {\bigl [}2\varphi -1+\varphi \alpha {\bigr ]}&{\Bigr )}\\{\Bigl (}&\pm {\bigl [}\varphi +1+\alpha {\bigr ]},&\pm \,2{\bigl [}\varphi -1{\bigr ]},&\pm {\bigl [}1+\varphi \alpha {\bigr ]}&{\Bigr )}\end{array}}}

where φ = 1 + 5 2 {\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}} is the golden ratio and α = 3 φ − 2 . {\displaystyle \alpha ={\sqrt {3\varphi -2}}.}

See also

External links


  • v
  • t
  • e