Notation de Voigt

Page d’aide sur l’homonymie

Pour les articles homonymes, voir Voigt.

Notation de Voigt pour une matrice symétrique 3x3.

On appelle notation de Voigt une convention permettant de réduire le nombre d'indices utilisés pour décrire un tenseur symétrique. Cette notation permet notamment de représenter sous forme matricielle des tenseurs d'ordre 3, comme le tenseur piézoélectrique, ou 4 comme le tenseur des modules élastiques. Cette notation doit son nom à Woldemar Voigt qui les a élaborées.

Principe et exemple

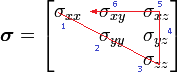
Le principe de la notation de Voigt est bien illustré par le cas des tenseurs symétriques de rang 2 tels que le tenseur des contraintes ou le tenseur des déformations. On représente un tel tenseur a i j {\displaystyle a_{ij}} par une matrice symétrique 3x3 :

( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) {\displaystyle \left({\begin{array}{c c c}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{array}}\right)}

Cette matrice contient 9 coefficients dont 6 seulement sont indépendants. La donnée de ces 6 coefficients suffit donc à représenter complètement le tenseur. On va donc rassembler les deux indices en un seul suivant la convention :

11 ⟶ 1 32   o u   23 ⟶ 4 22 ⟶ 2 31   o u   13 ⟶ 5 33 ⟶ 3 21   o u   12 ⟶ 6 {\displaystyle {\begin{aligned}11\longrightarrow 1\qquad \qquad 32\ \mathrm {ou} \ 23\longrightarrow 4\\22\longrightarrow 2\qquad \qquad 31\ \mathrm {ou} \ 13\longrightarrow 5\\33\longrightarrow 3\qquad \qquad 21\ \mathrm {ou} \ 12\longrightarrow 6\\\end{aligned}}}

Toutefois, il n'est pas possible de simplement remplacer les indices par les indices contractés. Afin de garder une représentation cohérente des propriétés physiques, il est nécessaire d'introduire quelques facteurs multiplicatifs. Ceci peut être mis en évidence sur un exemple. Considérons la loi de Hooke qui relie le tenseur des déformations ε i j {\displaystyle \varepsilon _{ij}} au tenseur des contraintes σ k l {\displaystyle \sigma _{kl}} par un tenseur des modules élastiques C i j k l {\displaystyle C_{ijkl}}  :

σ i j = C i j k l ε k l {\displaystyle \sigma _{ij}=C_{ijkl}\,\varepsilon _{kl}}

On écrira donc, par exemple pour σ 13 {\displaystyle \sigma _{13}}  :

σ 13 = C 1311 ε 11 + C 1322 ε 22 + C 1333 ε 33 + C 1332 ε 32 + C 1323 ε 23 ⏟ 2 C 1332 ε 32 + C 1331 ε 31 + C 1313 ε 13 ⏟ 2 C 1331 ε 31 + C 1312 ε 12 + C 1321 ε 21 ⏟ 2 C 1321 ε 21 {\displaystyle {\begin{aligned}\sigma _{13}=&\quad C_{1311}\,\varepsilon _{11}+C_{1322}\,\varepsilon _{22}+C_{1333}\,\varepsilon _{33}\\&+\underbrace {C_{1332}\,\varepsilon _{32}+C_{1323}\,\varepsilon _{23}} _{\displaystyle 2C_{1332}\,\varepsilon _{32}}+\underbrace {C_{1331}\,\varepsilon _{31}+C_{1313}\,\varepsilon _{13}} _{\displaystyle 2C_{1331}\,\varepsilon _{31}}+\underbrace {C_{1312}\,\varepsilon _{12}+C_{1321}\,\varepsilon _{21}} _{\displaystyle 2C_{1321}\,\varepsilon _{21}}\\\end{aligned}}}

Il est donc nécessaire de tenir compte de ces coefficients 2 en écrivant cette relation en indices contractés :

σ 5 = C 51 ε 1 + C 52 ε 2 + C 53 ε 3 + C 54 ε 4 + C 55 ε 5 + C 56 ε 6 {\displaystyle \sigma _{5}=C_{51}\,\varepsilon _{1}+C_{52}\,\varepsilon _{2}+C_{53}\,\varepsilon _{3}+C_{54}\,\varepsilon _{4}+C_{55}\,\varepsilon _{5}+C_{56}\,\varepsilon _{6}}

Dans le cas présent, ce coefficient 2 est intégré par convention dans la définition du tenseur des déformations, de sorte qu'on passe de la notation complète à la notation de Voigt par les relations suivantes, où l'on note les indices contractés par une lettre grecque :

σ α = σ i j C α β = C i j k l ε α = ε i j   p o u r   α = 1 , 2 , 3 = 2 ε i j   p o u r   α = 4 , 5 , 6 {\displaystyle {\begin{aligned}\sigma _{\alpha }&=\sigma _{ij}\\C_{\alpha \beta }&=C_{ijkl}\\\varepsilon _{\alpha }&=\varepsilon _{ij}\ \mathrm {pour} \ \alpha =1,2,3\\&=2\,\varepsilon _{ij}\ \mathrm {pour} \ \alpha =4,5,6\\\end{aligned}}}

Cas usuels

Le tableau suivant recense les cas usuels d'utilisation de la notation de Voigt.

Tenseur des déformations ε α = 2 p ε i j {\displaystyle \varepsilon _{\alpha }=2^{p}\,\varepsilon _{ij}}
Tenseur des contraintes σ α = σ i j   {\displaystyle \sigma _{\alpha }=\sigma _{ij}~}
Tenseurs piézoélectriques[1] d i α = 2 p d i ( j k ) ; e i α = e i ( j k ) {\displaystyle d_{i\alpha }=2^{p}\,d_{i(jk)}\quad ;\quad e_{i\alpha }=e_{i(jk)}}

g i α = 2 p g i ( j k ) ; h i α = h i ( j k ) {\displaystyle g_{i\alpha }=2^{p}\,g_{i(jk)}\quad ;\quad h_{i\alpha }=h_{i(jk)}}

Tenseur des constantes élastiques C α β = C ( i j ) ( k l )   {\displaystyle C_{\alpha \beta }=C_{(ij)(kl)}~}
Tenseur des compliances élastiques S α β = 2 p S ( i j ) ( k l ) {\displaystyle S_{\alpha \beta }=2^{p}\,S_{(ij)(kl)}}
À chaque fois, p {\displaystyle p} est le nombre d'indices contractés égaux à 4, 5 ou 6

Notes et références

  1. ↑ Il existe plusieurs représentations possibles du tenseur piézoélectrique. Ces notations sont les notations définies par les standards ANSI/IEEE (cf. Piézoélectricité).
  • (en) ANSI/IEEE Standard on Piezoelectricity, [détail de l’édition]


  • icône décorative Portail de la physique