Polygone de Newton

En mathématiques, le polygone de Newton est un polygone du plan euclidien que l'on peut associer à un polynôme, lorsque les coefficients de ce dernier sont éléments d'un corps valué. Le polygone de Newton encode un certain nombre d'informations à propos de la factorisation d'un polynôme, et la localisation de ses racines.

Il est particulièrement utile lorsque les coefficients du polynôme sont éléments d'un corps local non archimédien, comme le corps des nombres p-adiques, ou celui des séries de Laurent sur un corps fini, mais il peut également être utilisé avec profit dans l'étude des polynômes à coefficients rationnels, ou des polynômes en plusieurs indéterminées.

Construction

Soient (K,v) un corps valué, et P(X) un polynôme à coefficients dans K. Quitte à diviser P par une puissance de X, puis par P(0), on peut supposer que P(0) = 1, de sorte que P(X) s'écrive

${\displaystyle P(X)=1+a_{1}X+\cdots +a_{n}X^{n},}$

où les coefficients ${\displaystyle a_{1}}$, …, ${\displaystyle a_{n}}$ sont éléments de K, et ${\displaystyle a_{n}\neq 0}$ (ainsi, ${\displaystyle \deg(P)=n}$). Considérons l'ensemble S des points du plan

${\displaystyle A_{0}=(0,0)\quad {\text{et}}\quad A_{i}=(i,v(a_{i}))}$

pour ${\displaystyle 1\leqslant i\leqslant n}$, où l'on ignore les indices i pour lesquels ${\displaystyle a_{i}=0}$. Le polygone de Newton de P est alors la frontière inférieure de l'enveloppe convexe de cet ensemble S. Il s'agit donc d'une ligne brisée, réunion de segments dont les extrémités sont dans S.

En voici une construction plus explicite. Considérons l'axe des ordonnées, et faisons le tourner autour de l'origine ${\displaystyle A_{0}}$ dans le sens inverse des aiguilles d'une montre, jusqu'à ce qu'il rencontre l'un des points ${\displaystyle A_{i_{1}}}$ de S ; on obtient alors le premier segment ${\displaystyle [A_{i_{0}},A_{i_{1}}]}$ du polygone de Newton. Si l'on continue à faire tourner l'axe, autour du point ${\displaystyle A_{i_{1}}}$ cette fois, il finit par rencontrer un point ${\displaystyle A_{i_{2}}}$, et on obtient ainsi le second segment ${\displaystyle [A_{i_{1}},A_{i_{2}}]}$. En répétant cette opération autant de fois que possible, on finit par obtenir le polygone de Newton.

Remarques.

• Certains auteurs^[1] définissent le polygone de Newton comme la frontière supérieure de l'enveloppe convexe de l'ensemble des points ${\displaystyle (i,-v(a_{i}))}$. Les propriétés mentionnées dans la deuxième partie de cet article sont vraies quelle que soit la convention choisie, à la différence près qu'il faut changer le signe des pentes.
• D'autres auteurs considèrent que le polygone de Newton est l'enveloppe convexe de S, et non seulement sa frontière inférieure.

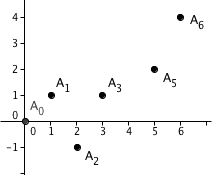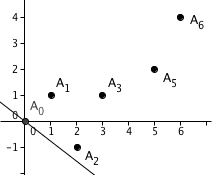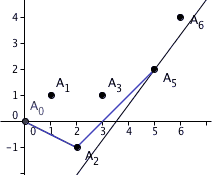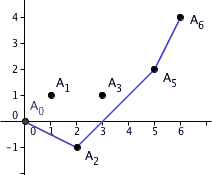
Exemple. Construisons le polygone de Newton du polynôme

${\displaystyle P(X)=1+5X+{\frac {1}{5}}X^{2}+35X^{3}+25X^{5}+625X^{6}}$

vu comme polynôme à coefficients dans le corps des nombres-p-adiques Q₅. La valuation que l'on utilise est donc la valuation 5-adique, et les points de l'ensemble S sont

${\displaystyle A_{0}=(0,0),\quad A_{1}=(1,1),\quad A_{2}=(2,-1),\quad A_{3}=(3,1),\quad A_{5}=(5,2),\quad A_{6}=(6,4).}$

Noter l'absence de ${\displaystyle A_{4}}$ dans cette liste, puisque le coefficient de ${\displaystyle X^{4}}$ dans P est nul. La construction du polynôme de Newton de P à partir de l'ensemble de points S est illustrée dans l'animation à droite. On voit qu'il s'agit de la ligne brisée de sommets ${\displaystyle A_{0}}$, ${\displaystyle A_{2}}$, ${\displaystyle A_{5}}$ et ${\displaystyle A_{6}}$.

Applications

Dans toute cette partie, P est un polynôme à coefficients dans K, et son polygone de Newton est composé de r segments ${\displaystyle [A_{0},A_{i_{1}}]}$, …, ${\displaystyle [A_{i_{r-1}},A_{i_{r}}]}$. On note ${\displaystyle m_{s}}$ la pente du s-ième segment (pour ${\displaystyle 1\leqslant s\leqslant r}$), et ${\displaystyle l_{s}}$ sa "longueur", c'est-à-dire la quantité ${\displaystyle i_{s}-i_{s-1}}$.

Factorisation dans les corps locaux

On considère ici le cas où ${\displaystyle (K,v)}$ est un corps local non archimédien, c'est-à-dire un corps de nombres p-adiques ou un corps ${\displaystyle \mathbf {F} _{q}((X))}$ de séries de Laurent sur un corps fini.

On dit^[2] que le polynôme ${\displaystyle \Pi }$ est pur de pente m lorsque son polygone de Newton est un unique segment dont la pente est m. Remarquons que dans ce cas, la pente est nécessairement ${\displaystyle v(a_{n})/n}$.

Le polygone de Newton d'un polynôme P (qui n'est pas a priori supposé pur) fournit les informations suivantes quant à sa factorisation dans ${\displaystyle K[X]}$.

En particulier, on peut facilement construire le polygone de Newton d'un polynôme irréductible.

Notons que la réciproque est fausse. En fait^[5], si f et g sont deux polynôme purs de même pente m, alors fg est lui aussi pur de pente m. Il existe cependant une réciproque partielle dans certains cas favorables (voir la section suivante).

Localisation des racines dans C_p

Dans cette partie on considère le cas où K est un corps de nombres p-adiques ${\displaystyle \mathbf {Q} _{p}}$, et v est donc la valuation p-adique ${\displaystyle v_{p}}$. Dans ce cadre, le polygone de Newton du polynôme P donne des informations précises quant à la localisation des racines de P dans ${\displaystyle \mathbf {C} _{p}}$.

On peut ainsi obtenir une réciproque partielle au corollaire donné dans la section précédente. Considérons ainsi le cas d'un polynôme ${\displaystyle P(X)\in \mathbf {Q} _{p}[X]}$ de degré n pur de pente m, et supposons en outre que ${\displaystyle v_{p}(a_{n})}$ est premier avec n. D'après le théorème qui précède, toutes les racines de P dans ${\displaystyle \mathbf {C} _{p}}$ ont pour valuation ${\displaystyle -v_{p}(a_{n})/n}$. Si l'on écrit ${\displaystyle P=QR}$, pour deux polynômes Q et R à coefficients dans ${\displaystyle \mathbf {Q} _{p}}$, avec Q de degré d, alors le produit des racines de Q a pour valuation ${\displaystyle -dv_{p}(a_{n})/n}$; or ce produit est (au signe près) le coefficient constant de Q, un élément de ${\displaystyle \mathbf {Q} _{p}}$, donc sa valuation est un entier. Ainsi, n divise ${\displaystyle dv_{p}(a_{n})}$ et est premier avec ${\displaystyle v_{p}(a_{n})}$, donc il divise d. On en déduit que P est irréductible, et on a par conséquent démontré le théorème suivant.

On retrouve comme cas particulier le critère d'Eisenstein, qui correspond au cas où ${\displaystyle v_{p}(a_{n})=-1}$. En effet, si P satisfait aux hypothèses du critère d'Eisenstein pour un nombre premier p, alors ${\displaystyle P(X)/a_{0}}$ a un coefficient constant égal à 1, le coefficient du terme dominant est ${\displaystyle 1/a_{0}}$, et les autres coefficients ont des valuations p-adiques positives. Le polynôme P est donc pur de pente ${\displaystyle -1/n}$.

Généralisations

Polynômes à plusieurs indéterminées

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Considérons un polynôme ${\displaystyle P(X,Y)}$ en deux indéterminées, à coefficients dans un corps K quelconque. On peut munir ${\displaystyle K(Y)}$ de la valuation la valuation Y-adique ${\displaystyle v_{Y}}$, définie pour un polynôme ${\displaystyle A(Y)=a_{0}+a_{1}Y+\cdots +a_{m}Y^{m}}$ comme le plus petit indice ${\displaystyle i}$ tel que ${\displaystyle a_{i}\neq 0}$, et étendue à ${\displaystyle K(Y)}$ en posant ${\displaystyle v_{Y}(A/B)=v_{Y}(A)-v_{Y}(B)}$. Le polygone de Newton d'un polynôme

${\displaystyle P(X,Y)=\sum a_{i,j}X^{i}Y^{j}}$

vis-à-vis de la valuation Y-adique est alors l'enveloppe convexe des points de coordonnées ${\displaystyle (i,j)}$ tels que ${\displaystyle a_{i,j}\neq 0}$.

Plus généralement, on peut construire le polytope de Newton d'un polynôme de ${\displaystyle K[X_{1},\ldots ,X_{n}]}$, comme ensemble convexe des points de ${\displaystyle \mathbf {R} ^{n}}$ de coordonnées ${\displaystyle (i_{1},\ldots ,i_{n})}$ tels que le coefficient devant ${\displaystyle X_{1}^{i_{1}}\cdots X_{n}^{i_{n}}}$ est non nul.

Séries formelles

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

On peut définir de la même façon le polygone de Newton d'une série formelle

${\displaystyle F=\sum _{i\geqslant 0}a_{i}X^{i}}$

à coefficients dans un corps valué ${\displaystyle (K,v)}$.

Voir aussi

• Critère d'Eisenstein
• Ramification

Notes

Références

• (en) Fernando Q. Gouvêa, p-adic Numbers: An Introduction [détail de l’édition] (Section 6.4)
• (en) J. W. S. Cassels, Local Fields [détail de l’édition] (Chapitre 6)

• Arithmétique et théorie des nombres