Tourbillons de Görtler

Les tourbillons de Görtler sont des tourbillons longitudinaux contrarotatifs par paire qui apparaissent dans une couche limite se développant sur une paroi concave. Ils ont été expliqués par Henry Görtler comme résultant de l'instabilité liée à l'accélération centrifuge^[1],[2].

Ces tourbillons interagissent avec les ondes de Tollmien-Schlichting, ce qui conduit à une transition laminaire-turbulent plus rapide que celle liée à l'instabilité naturelle, prédite par l'équation de Orr-Sommerfeld^[3],[4].

On constate expérimentalement que leur apparition est fortement dépendante de la turbulence en amont^[4].

Nombre de Görtler

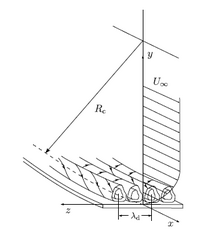
On part des équations de Navier-Stokes pour un écoulement incompressible de couche limite sur plaque plane, définie par les équations de Blasius dans un système curviligne lié à la paroi (voir figure) et défini par les variables (x, y, z). On définit une dimension caractéristique L par

${\displaystyle L={\sqrt {\frac {\nu x}{U_{\infty }}}}}$

Cette longueur est l'épaisseur de déplacement de la couche limite à un coefficient près^[5].

Le nombre de Reynolds vaut

${\displaystyle Re={\frac {U_{\infty }L}{\nu }}}$

avec

${\displaystyle U_{\infty }}$	vitesse hors couche limite
${\displaystyle \nu }$	viscosité cinématique
${\displaystyle x}$	distance à l'origine de la couche limite

Le rayon de courbure adimensionné  ${\displaystyle {\frac {R_{c}}{L}}}$  est supposé petit devant l'unité.

On définit le nombre de Görtler par

${\displaystyle G=Re\left({\frac {L}{R_{c}}}\right)^{1/2}}$

Ce nombre mesure donc les effets de la courbure par rapport aux effets visqueux.

Perturbations de la solution stationnaire

Comme dans tout problème de stabilité on superpose à la solution de base une perturbation dont on étudie l'évolution spatio-temporelle :

• la vitesse réduite par  ${\displaystyle U_{\infty }}$  a pour composantes  ${\displaystyle \mathbf {u} (\xi ,y)=[u(\xi ,y),v(\xi ,y),0]}$ : on lui superpose une perturbation  ${\displaystyle \mathbf {u} '(\xi ,y,z)=(u',v',w')}$  telle que  ${\displaystyle ||\mathbf {u} '||<<||\mathbf {u} ||}$,
• de la même façon la pression réduite par  ${\displaystyle \rho U_{\infty }^{2}}$  est perturbée par le terme  p' tel que  ${\displaystyle p'<<p}$.

En ne retenant que les termes du premier ordre le système s'écrit^[4],[6] :

${\displaystyle {\frac {\partial u'}{\partial \xi }}+{\frac {\partial v'}{\partial y}}+{\frac {\partial w'}{\partial z}}=0}$

${\displaystyle u{\frac {\partial u'}{\partial \xi }}+u'{\frac {\partial u}{\partial \xi }}+v{\frac {\partial u'}{\partial y}}+v'{\frac {\partial u}{\partial y}}-{\frac {\partial ^{2}u'}{\partial y^{2}}}-{\frac {\partial ^{2}u'}{\partial z^{2}}}=0}$

${\displaystyle u{\frac {\partial v'}{\partial \xi }}+u'{\frac {\partial v}{\partial \xi }}+v'{\frac {\partial v}{\partial y}}+v{\frac {\partial v'}{\partial y}}+2G^{2}uu'+{\frac {\partial p'}{\partial y}}-{\frac {\partial ^{2}v'}{\partial y^{2}}}-{\frac {\partial ^{2}v'}{\partial z^{2}}}=0}$

${\displaystyle u{\frac {\partial w'}{\partial \xi }}+v{\frac {\partial w'}{\partial y}}+{\frac {\partial p'}{\partial z}}-{\frac {\partial ^{2}w'}{\partial y^{2}}}-{\frac {\partial ^{2}w'}{\partial z^{2}}}=0}$

avec les conditions aux limites

${\displaystyle u'=v'=w'=0}$  pour ${\displaystyle y=0}$  et  ${\displaystyle y\to \infty }$

L'écriture fait apparaître le nombre de Görtler comme conséquence de l'adimensionnement. On remarque que dans les équations de conservation de quantité de mouvement l'évolution des composantes en y et z est couplée à la fluctuation de pression, mais pas celle en x, ce qui est cohérent avec la structure du tourbillon.

Ce système d'équations est de nature parabolique et peut donc être résolu par une marche en espace (calcul avançant plan par plan).

Résultats

Deux méthodes ont été utilisées pour résoudre le problème :

• dans la première on étudie la stabilité du système en utilisant une perturbation indépendante de x

${\displaystyle u'=u''(y)\cos(\alpha z)e^{\beta x}}$

${\displaystyle v'=v''(y)\cos(\alpha z)e^{\beta x}}$

${\displaystyle w'=w''(y)\sin(\alpha z)e^{\beta x}}$

${\displaystyle p'=p''(y)\cos(\alpha z)e^{\beta x}}$

où le nombre d'onde de la perturbation α (un paramètre du problème) est défini par

${\displaystyle \alpha ={\frac {2\pi L}{\lambda _{d}}}}$

β est solution du problème : β > 0 correspond à une solution crissante en x donc à une situation d'instabilité.

La méthode consiste alors à étudier les solutions du problème aux valeurs propres comme pour l'équation de Orr-Sommerfeld^[2].

• la seconde est une simulation directe par une marche en espace à partir d'une perturbation initiale raisonnablement choisie.

Ces deux méthodes donnent des résultats voisins : l'instabilité de Görtler apparaît pour G > 0.3 et pour les grandes longueurs d'onde. Les mesures en soufflerie conduisent à des valeurs notablement supérieures et notablement dépendantes des perturbations.

Références

Liens

• Portail de la physique