Trapézoèdre trigonal

Cet article est une ébauche concernant la géométrie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Trapézoèdre trigonal

Éléments

Faces	Arêtes	Sommets
6 losanges	12	8

Données clés

Type	Trapézoèdre
Caractéristique	2
Propriétés	convexe, isoédrique
Groupe de symétrie	D3d
Dual	antiprisme trigonal

modifier

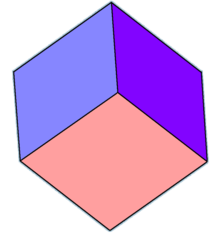
Le trapézoèdre trigonal ou rhomboèdre isoédrique est le premier cas de la série des trapézoèdres, polyèdres à faces isométriques et duaux des antiprismes. Il possède six faces qui sont des losanges isométriques. Il est le résultat de la déformation du cube dans la direction d'une grande diagonale.

C'est un cas particulier de rhomboèdre (parallélépipède à faces losanges qui peuvent être de trois formes différentes) lorsque les faces sont isométriques. Le cube en est un cas particulier lorsque les faces sont carrées.

Caractérisation et propriétés

• 
  Le trapézoèdre trigonal
• 
  et sa grande diagonale

Le trapézoèdre trigonal possède deux sommets où les trois angles des losanges y arrivant sont égaux, nommés ${\displaystyle \alpha }$ dans la figure ci-dessus. Les angles aux six autres sommets sont ${\displaystyle \alpha }$ et deux fois ${\displaystyle \pi -\alpha }$.

On peut caractériser le rhomboèdre, à isométrie près, par la longueur d'arête ${\displaystyle a}$ et l'angle ${\displaystyle \alpha }$, qui doit être strictement compris entre 0 et ${\displaystyle {\frac {2\pi }{3}}}$.

La diagonale joignant les deux sommets ci-dessus, de longueur ${\displaystyle a{\sqrt {3(1+2\cos \alpha )}}}$ est dite « grande diagonale » ; les trois autres sont de longueur ${\displaystyle a{\sqrt {3-2\cos \alpha }}}$.

Le volume est^[1] : ${\displaystyle V=a^{3}{\sqrt {1-3\cos ^{2}\alpha +2\cos ^{3}\alpha }}=a^{3}(1-\cos \alpha ){\sqrt {1+2\cos \alpha }}.}$

Le trapézoèdre trigonal présente un axe de symétrie ternaire (rotation d'ordre 3 - angle de 120°) dans la direction de sa plus grande diagonale. Vu dans cette direction :

• les trois arêtes qui partent du sommet le plus proche, projetées dans un plan perpendiculaire à la diagonale, forment entre elles un angle de 120° ;
• les 6 sommets qui n'appartiennent pas à la grande diagonale forment 2 triangles équilatéraux, situés respectivement dans 2 plans parallèles et perpendiculaires à la grande diagonale ; ces plans coupent cette diagonale aux 1/3 et 2/3 de sa hauteur.

Exemples

Un losange d'angle aigu ${\displaystyle \alpha }$ et d'angle obtus ${\displaystyle \beta =\pi -\alpha }$ donne naissance à un trapézoèdre trigonal ayant ce losange pour faces en réunissant trois angles aigus en un même sommet, et à un deuxième trapézoèdre en réunissant trois angles obtus en un même sommet. Ce deuxième trapézoèdre n'existe que si ${\displaystyle \beta <{\frac {2\pi }{3}}}$, soit ${\displaystyle \alpha >{\frac {\pi }{3}}}$.

C'est le cas, par exemple du losange d'or, qui a pour angles ${\displaystyle \alpha =2\arctan {1 \over \varphi }}$ et ${\displaystyle \beta =2\arctan \varphi }$, qui donne naissance à deux trapézoèdres trigonaux appelés rhomboèdres d'or^[2].

• 
  Rhomboèdre d'or aigu
• 
  Rhomboèdre d'or obtus

Références

Voir aussi

• L'hexacontaèdre rhombique, qui se décompose en 20 rhomboèdres d'or.

• Portail de la géométrie