Teorema Stokes rampat

Kalkulus
Teorema dasar Limit fungsi Kontinuitas Teorema nilai purata Teorema Rolle
Diferensial Definisi Turunan (perumuman) Tabel turunan Diferensial infinitesimal fungsi total Konsep Notasi untuk pendiferensialan Turunan kedua Turunan ketiga Perubahan variabel Pendiferensialan implisit Laju yang berkaitan Teorema Taylor Kaidah dan identitas Kaidah penjumlahan dalam pendiferensialan Perkalian Rantai Pangkat Pembagian Rumus Faà di Bruno
Integral Definisi Antiderivatif Integral (takwajar) Integral Riemann Integrasi Lebesgue Integrasi kontur Tabel integral Integrasi secara parsial cakram kulit tabung substitusi (trigonometri) pecahan parsial Urutan Rumus reduksi
Deret geometri (aritmetika-geometrik) harmonik selang-seling pangkat binomial Taylor Uji kekonvergenan uji suku rasio akar integral perbandingan langsung perbandingan limit deret selang-seling kondensasi Cauchy Dirichlet Abel
Vektor Gradien Divergence Keikalan Laplace berarah identitas Teorema Kedivergenan Gradien Green Stokes
Multivariabel Formalisme matriks tensor eksterior geometrik Definisi Turunan parsial Integral lipat Integral garis Permukaan integral integral volume Jacobi Hesse
Khusus fraksional Malliavin stokastik variasi
l b s

Dalam kalkulus vektor, dan lebih umum lagi geometri diferensial, teorema Stokes rampat (terkadang dieja teorema Stokes, dan juga disebut teorema Stokes–Cartan^[1]) adalah pernyataan tentang integrasi dari bentuk diferensial pada manifold, yang menyederhanakan dan menggeneralisasi beberapa teorema dari kalkulus vektor. Teorema Stokes mengatakan bahwa integral dari suatu bentuk diferensial ω di atas batas dari beberapa berorientasi lipatan Ω sama dengan integral turunan luar dω di seluruh Ω, yaitu:

${\displaystyle \int _{\partial \Omega }\omega =\int _{\Omega }d\omega \,.}$

Teorema Stokes 'dirumuskan dalam bentuk modern oleh Élie Cartan pada tahun 1945,^[2] mengikuti pekerjaan sebelumnya pada generalisasi teorema kalkulus vektor oleh Vito Volterra, Édouard Goursat, dan Henri Poincaré.^[3][4]

Bentuk modern dari teorema Stokes 'ini adalah generalisasi luas dari hasil klasik yang ditentukan oleh Lord Kelvin dikomunikasikan kepada George Stokes dalam surat tertanggal 2 Juli 1850.^[5][6][7] Stokes set the theorem as a question on the 1854 Smith's Prize exam, which led to the result bearing his name. It was first published by Hermann Hankel in 1861.^[7][8] Kelvin–Stokes teorema klasik tersebut menghubungkan integral permukaan dari curl dari bidang vektor F di atas permukaan (yaitu, fluks dari curl F) di Euclidean tiga ruang ke integral garis dari bidang vektor di atas batasnya (juga dikenal sebagai integral loop).

Contoh analisis vektor klasik sederhana

Mari γ: [a, b] → R² menjadi sedikit demi sedikit mulus kurva bidang Jordan. Teorema kurva Yordania menyiratkan hal itu γ membagi R² menjadi dua komponen, satu kompak satu sama lain yang tidak kompak. Membiarkan D menunjukkan bagian kompak yang dibatasi oleh γ dan misalkan ψ: D → R³ halus, dengan S := ψ(D). Jika Γ adalah kurva spasi yang ditentukan oleh Γ(t) = ψ(γ(t))^{[note 1]} dan F adalah bidang vektor mulus pada R³, kemudian:^[9][10][11]

${\displaystyle \oint _{\Gamma }\mathbf {F} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\nabla \times \mathbf {F} \,\cdot \,d\mathbf {S} }$

Pernyataan klasik ini, bersama dengan teorema divergensi klasik, teorema dasar kalkulus, dan Teorema Green hanyalah kasus-kasus khusus dari rumusan umum yang dinyatakan sebagai.

Pengantar

Teorema dasar kalkulus menyatakan bahwa integral dari suatu fungsi f selama interval [a, b] dapat dihitung dengan mencari antiturunan F of f:

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)\,.}$

Teorema Stokes adalah rampatan yang luas dari teorema ini dalam pengertian. Jadi, sama seperti seseorang dapat menemukan nilai integral (f dx = dF) di atas manifold 1 dimensi ([a, b]) dengan mempertimbangkan anti turunan (F) di batas 0-dimensi ({a, b}), seseorang dapat menggeneralisasi teorema dasar kalkulus, dengan beberapa peringatan tambahan, untuk menangani nilai integral (dω) di atas n-manifold dimensional (Ω) dengan mempertimbangkan antiturunan (ω) pada (n − 1)-batas dimensi (∂Ω) dari manifold tersebut.

Jadi teorema fundamental berbunyi:

${\displaystyle \int _{[a,b]}f(x)\,dx=\int _{[a,b]}dF=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.}$

Formulasi untuk lipatan halus dengan batas

Jadi Ω menjadi berorientasi lipatan halus dengan batas dimensi n dan biarkan α jadi polos n-bentuk diferensial yaitu didukung secara kompak aktif Ω. Pertama, anggap saja α didukung secara kompak dalam domain tunggal, berorientasi diagram koordinat {U, φ}. Dalam kasus ini, kami mendefinisikan integral dari α atas Ω sebagai

${\displaystyle \int _{\Omega }\alpha =\int _{\varphi (U)}\left(\varphi ^{-1}\right)^{*}\alpha \,,}$

yaitu, melalui pullback dari α ke Rⁿ.

Secara umum, integral dari α di atas Ω didefinisikan sebagai berikut: biar {ψ_i} menjadi partisi kesatuan terkait dengan terbatas lokal sampul {U_i, φ_i} dari bagan koordinat (berorientasi konsisten), lalu tentukan integralnya

${\displaystyle \int _{\Omega }\alpha \equiv \sum _{i}\int _{U_{i}}\psi _{i}\alpha \,,}$

di mana setiap suku dalam penjumlahan dievaluasi dengan menarik kembali ke Rⁿ seperti dijelaskan di atas. Kuantitas ini didefinisikan dengan baik; artinya, ini tidak bergantung pada pilihan bagan koordinat, atau pembagian kesatuan.

Teorema Stokes tergeneralisasi berbunyi:

Secara konvensional, ${\textstyle \int _{\partial \Omega }i^{*}\omega }$ disingkat sebagai ${\textstyle \int _{\partial \Omega }\omega }$, karena kemunduran bentuk diferensial oleh peta inklusi hanyalah pembatasannya pada domainnya: ${\displaystyle i^{*}\omega =\omega |_{\partial \Omega }}$. Saat ${\displaystyle d}$ adalah turunan eksterior, yang didefinisikan hanya dengan menggunakan struktur manifold. Sisi kanan terkadang ditulis sebagai ${\textstyle \oint _{\partial \Omega }\omega }$ untuk menekankan fakta bahwa ${\displaystyle (n-1)}$-manifold ${\displaystyle \partial \Omega }$ tidak memiliki batasan.^{[Catatan penting 1]} (Fakta ini juga merupakan implikasi dari teorema Stokes, karena untuk kelancaran tertentu ${\displaystyle n}$-berjenis dimensi ${\displaystyle \Omega }$, penerapan teorema dua kali memberi ${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$ untuk apapun ${\displaystyle (n-2)}$-bentuk ${\displaystyle \omega }$, yang menyiratkan itu ${\displaystyle \partial (\partial \Omega )=\emptyset }$.) Ruas kanan persamaan sering digunakan untuk merumuskan hukum integral; sisi kiri kemudian mengarah ke formulasi diferensial ekivalen (lihat di bawah).

The theorem is often used in situations where ${\displaystyle \Omega }$ is an embedded oriented submanifold of some bigger manifold, often ${\displaystyle \mathbf {R} ^{k}}$, on which the form ${\displaystyle \omega }$ is defined.

Pendahuluan topologi; integral melalui rantai

Maka M menjadi lipatan halus. Simpleks- k dengan M didefinisikan sebagai peta dari simplekd standar pada R^k ke M. Grup C_k(M, Z) dari singular kaidah- k pada M didefinisikan sebagai grup abelian bebas pada himpunan singular sederhana dalam M. Grup ini, dengan peta batas, ∂, mendefinisikan kompleks kaidah. Grup homologi (resp. Kohomologi) yang sesuai adalah isomorfik dari grup homologi tunggal biasa H_k(M, Z) (resp. grup kohomologi tunggal H^k(M, Z)), didefinisikan menggunakan kesederhanaan berkelanjutan dari M.

Di sisi lain, bentuk diferensial, dengan turunan eksterior, d, sebagai peta penghubung, membentuk kompleks cochain, yang mendefinisikan grup kohomologi de Rham HkdR(M, R).

Prinsip pendasar

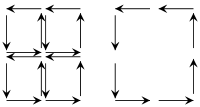
Untuk menyederhanakan argumen topologis ini, ada baiknya untuk memeriksa prinsip yang mendasari dengan mempertimbangkan contoh untuk dimensi d = 2. Ide esensial dapat dipahami dengan diagram di sebelah kiri, yang menunjukkan bahwa, dalam petak berorientasikan manifold, jalur interior dilintasi dalam arah yang berlawanan; kontribusi mereka ke integral jalan sehingga membatalkan satu sama lain secara berpasangan. Akibatnya, hanya kontribusi dari batas yang tersisa. Dengan demikian, cukup untuk membuktikan teorema Stokes untuk kemiringan yang cukup halus (atau, setara, sederhana), yang biasanya tidak sulit.

Rampat himpunan kasar

Rumus di atas, di mana Ω adalah lipatan halus dengan batas, tidak mencukupi dalam banyak aplikasi. Misalnya, jika domain integrasi didefinisikan sebagai bidang bidang antara dua koordinat x dan grafik dari dua fungsi, akan sering terjadi bahwa domain tersebut memiliki sudut. Dalam kasus, titik sudut berarti bahwa Ω bukan lipatan halus dengan batas, sehingga pernyataan teorema Stokes yang diberikan di atas tidak berlaku. Namun demikian, kesimpulan dari teorema Stokes. Ini karena Ω dan batasnya berperilaku baik menjauh dari sekumpulan kecil titik (himpunan mengukur nol).

Lihat pula

• Chandrasekhar–lemma Wentzel
• Portal:Matematika/Intro/Gambar
• Portal:Matematika/Templat halaman

Catatan kaki

Catatan penting

Referensi

Bacaan lebih lanjut

• Grunsky, Helmut (1983). The General Stokes' Theorem. Boston: Pitman. ISBN 0-273-08510-7. 
• Katz, Victor J. (May 1979). "The History of Stokes' Theorem". Mathematics Magazine. 52 (3): 146–156. doi:10.2307/2690275. JSTOR 2690275. 
• Loomis, Lynn Harold; Sternberg, Shlomo (2014). Advanced Calculus. Hackensack, New Jersey: World Scientific. ISBN 978-981-4583-93-0. 
• Madsen, Ib; Tornehave, Jørgen (1997). From Calculus to Cohomology: De Rham cohomology and characteristic classes. Cambridge, UK: Cambridge University Press. ISBN 0-521-58956-8. 
• Marsden, Jerrold E.; Anthony, Tromba (2003). Vector Calculus (edisi ke-5th). W. H. Freeman. 
• Lee, John (2003). Introduction to Smooth Manifolds. Springer-Verlag. ISBN 978-0-387-95448-6. 
• Rudin, Walter (1976). Principles of Mathematical Analysis. New York, NY: McGraw–Hill. ISBN 0-07-054235-X. 
• Spivak, Michael (1965). Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. San Francisco: Benjamin Cummings. ISBN 0-8053-9021-9. 
• Stewart, James (2009). Calculus: Concepts and Contexts. Cengage Learning. hlm. 960–967. ISBN 978-0-495-55742-5. 
• Stewart, James (2003). Calculus: Early Transcendental Functions (edisi ke-5th). Brooks/Cole. 
• Tu, Loring W. (2011). An Introduction to Manifolds (edisi ke-2nd). New York: Springer. ISBN 978-1-4419-7399-3. 

Pranala luar

• Hazewinkel, Michiel, ed. (2001) [1994], "Stokes formula", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Proof of the Divergence Theorem and Stokes' Theorem
• Calculus 3 – Stokes Theorem from lamar.edu – an expository explanation