Algoritmo di Frank-Wolfe

In ottimizzazione convessa vincolata e in analisi numerica, l'algoritmo di Frank-Wolfe (detto anche algoritmo del gradiente condizionale^[1], oppure del gradiente ridotto; in inglese conditional gradient o reduced gradient) è un metodo iterativo che consente di determinare il punto di minimo di un'approssimazione lineare della funzione obiettivo.

Il metodo fu sviluppato da Marguerite Frank e Philip Wolfe nel 1956^[2].

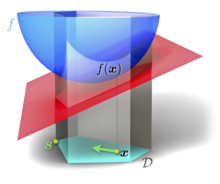
Sia ${\displaystyle D}$ un insieme convesso compatto in uno spazio vettoriale, e sia ${\displaystyle f\colon D\to \mathbb {R} }$ una funzione convessa e differenziabile. L'algoritmo di Frank-Wolfe trova ${\displaystyle \min _{\mathbf {x} \in D}f(\mathbf {x} )}$ in modo iterativo.

* Passo 0 (Inizializzazione): Si sceglie un punto ${\displaystyle \mathbf {x} _{0}\in D}$ e si pone ${\displaystyle k=0.}$
* Passo 1: Si determina ${\displaystyle \mathbf {s} _{k}=\min _{\mathbf {s} \in D}\mathbf {s} ^{T}\nabla f(\mathbf {x} _{k})}$.
* Passo 2: Si determina ${\displaystyle \alpha =\min _{0\leq \alpha \leq 1}f(\mathbf {x} _{k}+\alpha (\mathbf {s} _{k}-\mathbf {x} _{k}))}$.
* Passo 3: Si pone ${\displaystyle \mathbf {x} _{k+1}=\mathbf {x} _{k}+\alpha (\mathbf {s} _{k}-\mathbf {x} _{k})}$.
* Passo 4: Si pone ${\displaystyle k=k+1}$ e si torna al Passo 1.

A ogni iterazione l'algoritmo determina la direzione ${\displaystyle \mathbf {s} _{k}}$ e la dimensione del passo ${\displaystyle \alpha }$ lungo quella direzione in modo da minimizzare l'approssimazione lineare del problema. A differenza di metodi per l'ottimizzazione non vincolata, quali ad esempio la discesa del gradiente, l'algoritmo di Frank-Wolfe non necessita di proiezioni, poiché in ciascuna iterazione richiede soltanto la soluzione di un problema lineare sull'insieme ${\displaystyle D}$.

La convergenza dell'algoritmo di Frank-Wolfe è sublineare: l'errore nella funzione obiettivo è minimo dopo ${\displaystyle k}$ iterazioni, purché il gradiente sia Lipschitziano rispetto ad una norma.

• (EN) Jorge Nocedal e Stephen J. Wright, Numerical Optimization, 2ª ed., Berlino, Springer-Verlag, 2006, ISBN 978-0-387-30303-1.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica