Teorema del ballottaggio

Il teorema del ballottaggio prende il nome dal problema che originariamente si pone obiettivo di risolvere:
- Data un'elezione con voti validi e due soli candidati e che ricevono rispettivamente e , dove (e ), qual è la probabilità che, nello spoglio dei voti, risulti in ogni momento (a parte ovviamente che all'inizio) strettamente in vantaggio su ?
Questa probabilità è , ovvero, espressa in percentuale, , dove e sono rispettivamente le percentuali di voti di e .
Dimostrazione
Per dimostrare questo risultato, si può passare attraverso il principio di riflessione.
Sia (il numero di votanti). Partizioniamo , l'insieme di tutti i possibili scrutini (formalmente, di tutte le -uple ordinate di voti), in 3 sottoinsiemi:
- , che contiene tutti i possibili scrutini in cui il primo voto scrutinato va ad e che vedono, in un certo momento, una situazione di pareggio
- , che contiene tutti i possibili scrutini in cui il primo voto scrutinato va a (siccome A nel complesso ha ricevuto più voti, va da sé che anche in questi scrutini si assiste, prima o poi, ad almeno una situazione di pareggio)
- , che contiene tutti i possibili scrutini che vedono sempre in vantaggio (quelli che ci interessano)
Ad esempio, se prendiamo il caso in cui , e rappresentiamo ogni voto per con 1 e ogni voto per con -1 abbiamo che:
- (1 1 -1 -1 1 -1 1 1 1 1 -1) , perché 1+1-1-1=0,
- (-1 -1 1 -1 1 1 1 -1 1 1 1) , perché il primo voto è per (e infatti -1-1+1-1+1+1=0), mentre
- (1 1 -1 1 1 -1 1 -1 -1 1 1)
Si verifica facilmente che .
A questo punto prendiamo una qualsiasi -upla in . Supponiamo rappresenti uno scrutinio in cui la prima situazione di pareggio (può non essere l'unica) si realizzi dopo voti scrutinati. Se sostituiamo, nei primi campi della -upla, ogni 1 con un -1 e viceversa otteniamo una nuova ennupla che farà parte di (infatti questa sostituzione non altera il numero totale degli 1 e dei -1). Se invece applichiamo lo stesso procedimento ad un elemento di , otteniamo un elemento di . Si verifica facilmente che quella ora descritta è una corrispondenza biunivoca tra questi due sottoinsiemi, che quindi necessariamente hanno la stessa cardinalità. Ovvero la probabilità che, scelto uno scrutinio possibile a caso, questo faccia parte di , è uguale alla probabilità che faccia parte di (formalmente, questo si giustifica utilizzando la probabilità uniforme sull'insieme delle -uple a termini +1 e -1).
-
 Grafico dell'andamento dello scrutinio per una n-upla appartenente a .
Grafico dell'andamento dello scrutinio per una n-upla appartenente a . -
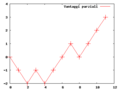 Grafico dell'andamento dello scrutinio per una n-upla appartenente a .
Grafico dell'andamento dello scrutinio per una n-upla appartenente a . -
 Grafico dell'andamento dello scrutinio per una n-upla appartenente a .
Grafico dell'andamento dello scrutinio per una n-upla appartenente a . -
 Riflettendo una n-upla appartenente a , ne otteniamo una appartenente a .
Riflettendo una n-upla appartenente a , ne otteniamo una appartenente a .
Ora non è difficile calcolare la probabilità che uno scrutinio scelto a caso faccia parte di , perché è semplicemente la probabilità che il primo voto scrutinato sia per , ovvero , che è anche la probabilità che lo scrutinio faccia parte di . La probabilità che non faccia parte di nessuno dei due, e che quindi faccia parte di , è: .
Un altro modo classico per dimostrare questo risultato sfrutta il principio di induzione.
Storia
Del problema del ballottaggio sono state studiate svariate generalizzazioni, in due direzioni:
- i candidati non sono 2 ma un qualsiasi numero ( con rispettivamente voti a testa)
- la differenza di consensi tra i due candidati non è espressa come differenza di voti o come percentuale ma come rapporto del numero di voti ottenuti (il candidato ha volte più voti di )
Il teorema del ballottaggio viene spesso associato al nome di Joseph Louis François Bertrand, matematico francese del XIX secolo.
La rovina del giocatore
In uno spoglio già iniziato, in cui goda un margine di un vantaggio esiguo (rispetto al numero di voti ancora da scrutinare), la possibilità per di tornare momentaneamente in parità dipende da una dinamica simile a quella della rovina del giocatore, dove la probabilità, ad ogni estrazione, di una "vincita" per è approssimabile con il rapporto tra il numero di voti ancora da scrutinare di e quelli di : tuttavia, questa probabilità decresce con il procedere dello scrutinio, e la possibilità che il candidato torni in parità diventa nulla quando restano da scrutinare solo voti.
Altri progetti
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su teorema del ballottaggio
Wikimedia Commons contiene immagini o altri file su teorema del ballottaggio
Collegamenti esterni
- (EN) Eric W. Weisstein, Teorema del ballottaggio, su MathWorld, Wolfram Research.

 Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica
Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica










































