オートエンコーダ

機械学習および データマイニング
問題 分類 クラスタリング 回帰 異常検知 相関ルール（英語版） 強化学習 構造化予測（英語版） 特徴量設計（英語版） 表現学習（英語版） オンライン学習（英語版） 半教師あり学習（英語版） 教師なし学習 ランキング学習（英語版） 文法獲得（英語版）
教師あり学習（分類 • 回帰） 決定木（英語版） アンサンブル （バギング、ブースティング、 ランダムフォレスト） k-NN 線形回帰 単純ベイズ ニューラルネットワーク ロジスティック回帰 パーセプトロン 関連ベクトルマシン (RVM)（英語版） サポートベクトルマシン (SVM)
クラスタリング BIRCH（英語版） 階層的（英語版） k平均法 期待値最大化法 (EM) DBSCAN OPTICS（英語版） 平均値シフト（英語版）
次元削減 因子分析 CCA ICA LDA（英語版） NMF（英語版） PCA t-SNE
構造化予測（英語版） グラフィカルモデル ベイジアンネットワーク CRF HMM
異常検知 k-NN 局所外れ値因子法
ニューラルネットワーク オートエンコーダ ディープラーニング DeepDream 多層パーセプトロン RNN LSTM GRU 制約ボルツマンマシン（英語版） SOM CNN U-Net
強化学習 TD学習 Q学習 SARSA
理論 偏りと分散のトレードオフ 計算論的学習理論（英語版） 経験損失最小化（英語版） オッカム学習（英語版） PAC学習 統計的学習（英語版） VC理論（英語版）
学会・論文誌等 NIPS（英語版） ICML（英語版） ML（英語版） JMLR（英語版） ArXiv:cs.LG
全般 統計学および機械学習の評価指標
Category:機械学習 Category:データマイニング
表 話 編 歴

オートエンコーダ（自己符号化器、英: autoencoder）とは、機械学習において、ニューラルネットワークを使用した次元圧縮のためのアルゴリズム。2006年にジェフリー・ヒントンらが提案した^[1]。

概要

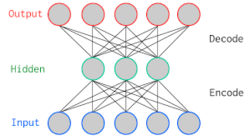
オートエンコーダは3層ニューラルネットにおいて、入力層と出力層に同じデータを用いて教師なし学習させたものである。教師データが実数値で値域がない場合、出力層の活性化関数は恒等写像、（すなわち出力層は線形変換になる）が選ばれることが多い。中間層の活性化関数も恒等写像を選ぶと結果は主成分分析とほぼ一致する。実用上では、入力と出力の差分をとることで、異常検知に利用されている。

特性と限界

オートエンコーダは次元圧縮に必要な特性を有するように設計されている。

オートエンコーダは中間層の次元数 ${\displaystyle d_{m}}$ が入出力層の次元数 ${\displaystyle d_{i,o}}$ より小さいように制約されている。なぜなら ${\displaystyle d_{i,o}\leqq d_{m}}$ の場合、オートエンコーダは恒等変換のみで再構成誤差ゼロを達成できてしまう^[2]。

オートエンコーダは次元圧縮を実現するが、これは良い表現学習を必ずしも意味しない^[3]。${\displaystyle d_{m}}$ を小さくすることで入力中の情報量が多い（より少量で画像を再構成できる）特徴のみが保存されると期待されるが（c.f. 非可逆圧縮）、これが特徴量として優れているとは一概に言えない。

理論

AEが再構成および次元圧縮を学習できる理由が理論的に解析されている。

オートエンコーダネットワーク ${\displaystyle AE_{\phi ,\theta }(x)}$ はエンコーダネットワーク ${\displaystyle NN_{\phi }(x)}$ とデコーダネットワーク ${\displaystyle NN_{\theta }(x)}$ からなる。決定論的な解釈においてAEは「再構成された入力」を直接出力する。すなわち ${\displaystyle {\hat {x}}=AE_{\phi ,\theta }(x)=NN_{\theta }(NN_{\phi }(x))}$ である。

確率論的解釈

AEは確率モデルの観点から深層潜在変数モデルの一種とみなせ、次のように定式化できる：

${\displaystyle {\begin{aligned}z_{|x}\sim p_{\phi }(Z|X)&=p(Z|\lambda =NN_{\phi }(X))=\delta (Z-NN_{\phi }(X))\\{\hat {x}}_{|z}\sim p_{\theta }({\hat {X}}|Z)&=p({\hat {X}}|\mu =NN_{\theta }(Z))\end{aligned}}}$

すなわち ${\displaystyle NN_{\phi }(x),NN_{\theta }(x)}$ は分布パラメータ ${\displaystyle \lambda ,\mu }$ を出力し分布を介して ${\displaystyle z,{\hat {x}}}$ が得られると解釈できる^[4][5]。AEではエンコーダが決定論的に振舞うため、写像の条件付き確率分布（デルタ関数 ${\displaystyle \delta }$）で表現される。${\displaystyle \delta }$ の決定論的性質より ${\displaystyle NN_{\phi }(x),NN_{\theta }(x)}$ を集約して表現するとAEは次の確率論的表現で表される：

${\displaystyle {\hat {x}}_{|x}\sim p({\hat {X}}|\mu =AE_{\phi ,\theta }(X))}$

AEの学習には平均二乗誤差（MSE, L₂）をはじめ様々な損失関数が（決定論的な視点から）経験的に使われている。これは経験的なものであって学習収束保証があるとは限らない。理論的な研究により、いくつかの損失関数では ${\displaystyle p_{\theta }({\hat {X}}|Z)}$ に特定の分布を設定したinfomax学習として定式化できることがわかっている。

固定分散正規分布モデル

「分散が固定された正規分布 ${\displaystyle N(X|\mu _{\theta },\sigma )}$」を考えると負の対数尤度 ${\displaystyle L_{n}(\theta )}$ は以下になる：

${\displaystyle L_{n}(\theta )={\frac {\|x-\mu _{\theta }\|^{2}}{2\sigma ^{2}}}-\log({\sqrt {2\pi \sigma ^{2}}})\propto \|x-\mu _{\theta }\|^{2}}$

これは ${\displaystyle x}$ と ${\displaystyle \mu _{\theta }}$ の二乗誤差と解釈できる。すなわち、 ${\displaystyle N(X|\mu _{\theta }=AE_{\phi ,\theta }(x),\sigma )}$ のNLL最小化と ${\displaystyle {\hat {x}}=AE_{\phi ,\theta }(x)}$ の二乗誤差最小化は同等とみなせる^[6]。換言すれば、二乗誤差で学習されたオートエンコーダモデルは「最尤推定された固定分散正規分布 ${\displaystyle N(X|\mu _{\theta }=AE_{\phi ,\theta }(x),\sigma )}$ からの最頻値サンプリングモデル」であるとみなせる。

派生

オートエンコーダには様々な変種・派生モデルが存在する。以下はその一例である：

• 変分オートエンコーダー（VAE）
• Contractive AutoEncoder
• Saturating AutoEncoder
• Nonparametrically Guided AutoEncoder
• Unfolding Recursive AutoEncoder

スパース・オートエンコーダ

スパース・オートエンコーダ（英: sparse autoencoder）とは、フィードフォワードニューラルネットワークの学習において汎化能力を高めるため、正則化項を追加したオートエンコーダのこと。ただし、ネットワークの重みではなく、中間層の値自体を0に近づける。

Stacked autoencoder

バックプロパゲーションでは通常、中間層が2層以上ある場合、極小解に収束してしまう。そこで、中間層1層だけでオートエンコーダを作って学習させる。次に、中間層を入力層と見なしてもう1層積み上げる。これを繰り返して多層化したオートエンコーダをつくる方法をstacked autoencoderと言う。

Denoising AutoEncoder

入力層のデータにノイズを加えて学習させたもの。制約付きボルツマンマシンと結果がほぼ一致する。ノイズは確率分布が既知であればそれに従ったほうが良いが、未知である場合は一様分布で良い。

類似技術

• ディープビリーフネットワーク
• ディープボルツマンマシン

脚注

出典