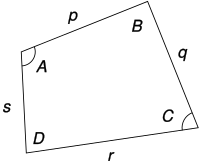
p , q , r , s , A , C の値から四角形の面積が求まる。ブレートシュナイダーの公式 (ブレートシュナイダーのこうしき、Bretschneider's formula)は、四角形 の面積を与える公式である。四角形ABCD について、p , q , r , s をそれぞれの辺の長さ、T を半周長 、A と C を互いに対角とすると、四角形の面積は
( T − p ) ( T − q ) ( T − r ) ( T − s ) − p q r s cos 2 A + C 2 {\displaystyle {\sqrt {(T-p)(T-q)(T-r)(T-s)-pqrs\cos ^{2}{\frac {A+C}{2}}}}} に等しい。円に内接する四角形の面積を表したブラーマグプタの公式 の一般化であり、任意の四角形について成り立つ。名前の由来はドイツ の数学者 カール・アントン・ブレートシュナイダー(1808–1878)にちなむ。
証明 四角形の面積を S とすると、
S = ± △ ADB ± △ BDC {\displaystyle S=\pm \bigtriangleup {\text{ADB}}\pm \bigtriangleup {\text{BDC}}} = 1 2 p s sin A + 1 2 q r sin C {\displaystyle {\begin{aligned}&={\frac {1}{2}}ps\sin A+{\frac {1}{2}}qr\sin C\end{aligned}}} より
4 S 2 = ( p s ) 2 sin 2 A + ( q r ) 2 sin 2 C + 2 p q r s sin A sin C {\displaystyle 4S^{2}=(ps)^{2}\sin ^{2}A+(qr)^{2}\sin ^{2}C+2pqrs\sin A\sin C} を得る。また、余弦定理 より、
BD 2 = p 2 + s 2 − 2 p s cos A = q 2 + r 2 − 2 q r cos C {\displaystyle {\text{BD}}^{2}=p^{2}+s^{2}-2ps\cos A=q^{2}+r^{2}-2qr\cos C} であるから
1 4 ( q 2 + r 2 − p 2 − s 2 ) 2 = ( p s ) 2 cos 2 A + ( q r ) 2 cos 2 C − 2 p q r s cos A cos C {\displaystyle {\frac {1}{4}}(q^{2}+r^{2}-p^{2}-s^{2})^{2}=(ps)^{2}\cos ^{2}A+(qr)^{2}\cos ^{2}C-2pqrs\cos A\cos C} を得る。4S 2 についての式と辺々を足し合わせ、加法定理 cos(A + C ) = cos A cos C − sin A sin C を用いると、
4 S 2 + 1 4 ( q 2 + r 2 − p 2 − s 2 ) 2 = ( p s ) 2 + ( q r ) 2 − 2 p q r s cos ( A + C ) {\displaystyle 4S^{2}+{\frac {1}{4}}(q^{2}+r^{2}-p^{2}-s^{2})^{2}=(ps)^{2}+(qr)^{2}-2pqrs\cos(A+C)} となる。倍角の公式 1 + cos θ = 2 cos 2 θ 2 {\displaystyle 1+\cos \theta =2\cos ^{2}{\frac {\theta }{2}}}
16 S 2 = ( p + q + r − s ) ( p + q − r + s ) ( p − q + r + s ) ( − p + q + r + s ) − 16 p q r s cos 2 A + C 2 {\displaystyle 16S^{2}=(p+q+r-s)(p+q-r+s)(p-q+r+s)(-p+q+r+s)-16pqrs\cos ^{2}{\frac {A+C}{2}}} となる。この式は、半周長
T = p + q + r + s 2 {\displaystyle T={\frac {p+q+r+s}{2}}} を用いて
16 S 2 = 16 ( T − p ) ( T − q ) ( T − r ) ( T − s ) − 16 p q r s cos 2 A + C 2 {\displaystyle 16S^{2}=16(T-p)(T-q)(T-r)(T-s)-16pqrs\cos ^{2}{\frac {A+C}{2}}} となり、ブレートシュナイダーの公式を得る。
関連する公式 円に内接する四角形については、対角の和の半分が 90°であることから、ブラーマグプタの公式
S = √ (T − p )(T − q )(T − r )(T − s ) が成り立つ。また、円に外接する四角形については、対辺の和が等しく、T = p + r = q + s
S = p q r s sin A + C 2 {\displaystyle S={\sqrt {pqrs}}\sin {\frac {A+C}{2}}} が成り立つ。さらに外接円と内接円を持つ四角形、つまり双心四角形 については、
S = √ pqrs となる。また、上記の証明は p = 0ヘロンの公式
S = √ T (T − q )(T − r )(T − s )を得る。
脚注 [脚注の使い方 ]
参考文献 E. A. José García (2020) (英語). Two Identities and their Consequences . MATINF. pp. 5-11. http://matinf.upit.ro/MATINF6/index.html?fbclid=IwAR1l1rO0oOyEFW8UHuh5Mlt3gv_w8ibykYZGbVM7x2EKG7t3rHSc-vSMH7A#p=1 アーネスト・ウィリアム・ホブソン (1918) (英語). A Treatise on Plane Trigonometry . Cambridge University Press. https://archive.org/details/treatiseonplanet00hobs/page/n7/mode/2up 関連項目 外部リンク 『ブレートシュナイダーの公式』 - 高校数学の美しい物語 Weisstein, Eric W. "Bretschneider's formula". mathworld.wolfram.com (英語).