Elipse

 Nota: Para outros significados, veja Elipse (desambiguação).
Uma elipse é a intersecção de uma superfície cônica com um plano que a corta numa curva fechada.

Em geometria, uma elipse é um tipo de seção cônica: se uma superfície cônica é cortada com um plano que não passe pela base e que não intersete as duas folhas do cone, a interseção entre o cone e o plano é uma elipse. Para uma prova elementar disto, veja esferas de Dandelin.

Em alguns contextos, pode-se considerar o círculo e o segmento de reta como casos especiais de elipses; no caso do círculo, o plano que corta o cone é paralelo à sua base.

A elipse tem dois focos, que no caso do círculo são sobrepostos. O segmento de reta que passa pelos dois focos chama-se eixo maior, e o segmento de reta que passa pelo ponto médio do eixo maior e é perpendicular a ele chama-se eixo menor. Fixando o comprimento do eixo maior e diminuindo o comprimento do eixo menor, obtêm-se elipses cada vez mais próximas de um segmento de reta. A elipse é também a intersecção de uma superfície cilíndrica com um plano que a corta numa curva fechada.

As medidas da elipse são dadas pela metade dos eixos maior e menor sendo chamadas, respetivamente, de semieixo maior ( a {\displaystyle a} ) e semieixo menor ( b {\displaystyle b} ).

Equações

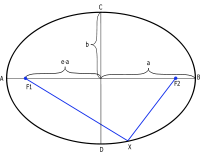
Uma elipse e algumas de suas propriedades. c = a ⋅ e {\displaystyle c=a\cdot e}

Coordenadas cartesianas

Ver artigos principais: Sistema de coordenadas cartesiano e Sistema de coordenadas

Algebricamente, uma elipse é a curva no plano cartesiano definida por uma equação da forma

A x 2 + B x y + C y 2 + D x + E y + F = 0 {\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}

tal que

B 2 < 4 A C , {\displaystyle B^{2}<4AC,}
onde todos os coeficientes são reais, e onde mais de uma solução, definindo um par de pontos ( x , y {\displaystyle x,y} ) na elipse, existe. O caso A = C , A ≠ 0 , B = 0 {\displaystyle A=C,A\neq 0,B=0} corresponde ao círculo. Quando os eixos da elipse são paralelos aos eixos coordenados, a equação anterior torna a forma mais simples:

( x − h a ) 2 + ( y − k b ) 2 = 1 , {\displaystyle \left({\frac {x-h}{a}}\right)^{2}+\left({\frac {y-k}{b}}\right)^{2}=1,}

onde ( h , k {\displaystyle h,k} ) é o centro da elipse, e a {\displaystyle a} e b {\displaystyle b} são os semieixos da elipse.

Outras equações úteis:

1) Centro na origem:

a) Eixo maior paralelo ao eixo x : {\displaystyle x:} x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}

b) Eixo maior paralelo ao eixo y : {\displaystyle y:} x 2 b 2 + y 2 a 2 = 1 {\displaystyle {\frac {x^{2}}{b^{2}}}+{\frac {y^{2}}{a^{2}}}=1}

2) Centro como um vértice, geralmente apresentado como C   ( h , k ) : {\displaystyle C~(h,k):}

a) Eixo maior paralelo ao eixo x : {\displaystyle x:} ( x − h ) 2 a 2 + ( y − k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}

b) Eixo maior paralelo ao eixo y : {\displaystyle y:} ( x − h ) 2 b 2 + ( y − k ) 2 a 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{b^{2}}}+{\frac {(y-k)^{2}}{a^{2}}}=1}

Coordenadas polares

Em coordenadas polares, existem duas formas principais de se descrever a elipse:

a) Com origem no centro da elipse: r = a b a 2 sen 2 ⁡ θ + b 2 cos 2 ⁡ θ {\displaystyle r={\frac {ab}{\sqrt {a^{2}\operatorname {sen} ^{2}\theta +b^{2}\cos ^{2}\theta }}}}

b) Com origem em um dos focos: r = a ( 1 − e 2 ) 1 + e cos ⁡ θ , {\displaystyle r={\frac {a(1-e^{2})}{1+e\cos \theta }},} sendo e a excentricidade.

Essa forma é muito conveniente para aplicações em mecânica celeste, neste caso o ângulo θ {\displaystyle \theta } é chamado de anomalia verdadeira e é representado pela letra grega ν {\displaystyle \nu } (nu ou ni)

Coordenadas paramétricas

{ x = h + a . cos ⁡ ( t ) y = k + b . sen ⁡ ( t ) {\displaystyle \left\{{\begin{matrix}x&=&h+a.\cos(t)\\y&=&k+b.\operatorname {sen} (t)\end{matrix}}\right.}

A elipse como lugar geométrico

A elipse pode ser construída usando-se dois pregos, um barbante e um lápis.

A elipse é o conjunto dos pontos P {\displaystyle P} do plano tais que a soma das distâncias de P {\displaystyle P} a dois pontos fixos F 1   e   F 2 {\displaystyle F_{1}~e~F_{2}} (focos) é constante. O teorema de Dandelin mostra que esta caracterização da elipse é equivalente à definição como secção cónica.

Ou seja, se d i s t ( F 1 , F 2 ) = 2 c , {\displaystyle dist(F_{1},F_{2})=2c,} então a elipse é o conjunto dos pontos P {\displaystyle P} tais que d i s t ( P , F 1 ) + d i s t ( P , F 2 ) = 2 a {\displaystyle dist(P,F_{1})+dist(P,F_{2})=2a} em que a > c {\displaystyle a>c} (no caso especial do círculo, os pontos F 1   e   F 2 {\displaystyle F_{1}~e~F_{2}} coincidem então c = 0   e   a = r , {\displaystyle c=0~e~a=r,} com r {\displaystyle r} sendo o raio do círculo).

A excentricidade da elipse é definida por e = c a . {\displaystyle e={\frac {c}{a}}.} A excentricidade também pode ser calculada pelo ângulo característico ( α {\displaystyle \alpha } ) da elipse.[1]

e = 2 ⋅ c o s ( α ) 1 + c o s ( α ) {\displaystyle e={\sqrt {\tfrac {2\cdot cos(\alpha )}{1+cos(\alpha )}}}}

Tem-se 0 ≤ e < 1 {\displaystyle 0\leq e<1} (de novo, e = 0 {\displaystyle e=0} apenas no caso da circunferência, o caso e = 1 {\displaystyle e=1} corresponderia ao segmento de reta, mas normalmente e = 1 {\displaystyle e=1} corresponde a uma parábola). Se a {\displaystyle a} for o semi-eixo maior e b {\displaystyle b} o semi-eixo menor da elipse, então pelo teorema de Pitágoras vem

e = a 2 − b 2 a {\displaystyle e={\frac {\sqrt {{a^{2}}-{b^{2}}}}{a}}}

Em geodésia e cartografia, é usado o conceito de achatamento (para se referir ao elipsoide de referência), definido por f = ( a − b ) a . {\displaystyle f={\frac {(a-b)}{a}}.} Como este valor é sempre muito pequeno, ele costuma ser apresentado por seu inverso. Por exemplo, o achatamento do WGS 1984 é 1 298.257223563 . {\displaystyle {\frac {1}{298.257223563}}.}

Características

A B ¯ = 2 a = Eixo   Maior, {\textstyle {\overline {AB}}=2a={\textrm {Eixo}}\ {\textrm {Maior,}}} C D ¯ = 2 b = Eixo   Menor, {\textstyle {\overline {CD}}=2b={\textrm {Eixo}}\ {\textrm {Menor,}}}

F 1 F 2 ¯ = 2 c = Distancia   Focal. {\textstyle {\overline {F_{1}F_{2}}}=2c={\textrm {Distancia}}\ {\textrm {Focal.}}}

O centro da elipse é ponto O = ( 0 , 0 ) {\displaystyle O=(0,0)} . Os focos da elipse encontram-se nos pontos:

F 1 = ( − c , 0 )   e   F 2 = ( c , 0 ) . {\displaystyle F_{1}=(-c,0)\ {\textrm {e}}\ F_{2}=(c,0).}

Temos, pelo Teorema de Pitágoras aplicado ao triângulo retângulo C O F 2 {\displaystyle COF_{2}} (ou ao C O F 1 , {\displaystyle COF_{1},} ou ainda ao D O F 2 {\displaystyle DOF_{2}} ), que:

a 2 = b 2 + c 2 {\displaystyle a^{2}=b^{2}+c^{2}}

Este resultado decorre da definição da elipse: a soma das distâncias de qualquer ponto P {\displaystyle P} sobre a elipse até os focos é sempre 2 a {\displaystyle 2a} . Em símbolos:

P F 2 ¯ + P F 1 ¯ = 2 a {\displaystyle {\overline {PF_{2}}}+{\overline {PF_{1}}}=2a}

Então, utilizando seguimentos de retas iguais, temos:

C F 1 ¯ + C F 2 ¯ = 2 a ⇒ C F 1 ¯ = a ou D F 1 ¯ + D F 2 ¯ = 2 a ⇒ D F 1 ¯ = a {\displaystyle {\overline {CF_{1}}}+{\overline {CF_{2}}}=2a\Rightarrow {\overline {CF_{1}}}=a\,\,{\textrm {ou}}\,\,{\overline {DF_{1}}}+{\overline {DF_{2}}}=2a\Rightarrow {\overline {DF_{1}}}=a}

o símbolo matemático " ⇒ {\displaystyle \Rightarrow } " significa "implica".

Área

A área de uma elipse com semieixo maior a {\displaystyle a} e semieixo menor b {\displaystyle b} é igual a π a b {\displaystyle \pi ab} (semieixo significa metade do eixo). Se a excentricidade da elipse é nula, os semieixos são iguais ( a = b = r ) , {\displaystyle (a=b=r),} ficamos então com um círculo de raio r . {\displaystyle r.} Neste caso, a fórmula da área resulta na expressão mais conhecida para a área de um círculo: π a b = π r r = π r 2 . {\displaystyle \pi ab=\pi rr=\pi r^{2}.}

Propriedade refletora

As linhas FM e F'M formam ângulos iguais com a tangente à elipse no ponto M.

A elipse tem a propriedade de que a bissectriz do ângulo formado pelos dois focos e por um ponto qualquer da elipse (como vértice) é perpendicular à tangente à elipse nesse ponto.

Como consequência, qualquer raio luminoso ou onda sonora, que parta de um dos focos, será reflectido pela elipse na direcção do outro foco.

Particularidades

Segundo esta propriedade, numa mesa de bilhar elíptica, qualquer choque entre duas bolas, acontecido num foco, será refletido e fará bater em uma terceira bola estacionada no outro foco.

Num plano de três dimensões, esse é o princípio da sala de sussurro que existe em museus e exposições: duas pessoas estacionadas nos focos de um elipsoide podem conversar entre si em voz baixa e mesmo assim serem ouvidas por uma pessoa estacionada no outro foco. No Capitólio dos Estados Unidos há uma sala elíptica onde a propriedade refletora da elipse teria sido usada pelo presidente John Quincy Adams para escutar conversas que decorriam do outro lado da sala.

Outro fato curioso sobre as elipses é que, trabalhando com sua excentricidade ( e = c a {\displaystyle e={\frac {c}{a}}} ), podemos obter tanto circunferências (casos de excentricidade nula e, portanto, com distância focal igual a zero) quanto segmentos de reta (casos de excentricidade igual a 1 , {\displaystyle 1,} ou seja, a distância focal coincide com o tamanho do eixo maior).

O acompanhamento por telescópio do reflexo da intensa luminosidade de uma supernova nos gases e poeira que se encontram sobre o elipsoide, cujos focos são a supernova e a Terra, tem permitido compreender melhor a estrutura do meio interestelar.[2]

Primeira lei de Kepler

A primeira lei de Kepler afirma que a órbita dos planetas em redor do Sol é elíptica, estando o Sol num dos focos. Dos seis elementos orbitais necessários para descrever completamente a órbita do planeta dois são os parâmetros que definem a elipse.

Ver também

Referências

  1. ↑ Brito, H.; Santos, M. A. C.; Mendes, R. L. T.; Matos, F. C. (2020). «Novas abordagens no estudo das elipses». In: Silva, A. J. N. A Educação enquanto Fenômeno Social: Política, Economia, Ciência e Cultura. 3. Ponta Grossa: Atena. ISBN 978-65-5706-533-4. doi:10.22533/at.ed.33420051116. Consultado em 26 de novembro de 2020  !CS1 manut: número-autores (link)
  2. ↑ Ecos de antigas supernovas (em inglês)inglês)inglês)

Bibliografia

  • Braga, Theodoro - Desenho linear geométrico. Ed. Cone, São Paulo: 1997 ISBN 8-527-40497-4 .
  • A. Carvalho, Benjamim - Desenho Geométrico. Ed. Ao Livro Técnico, São Paulo: 1982 OCLC 46751346.
  • Giongo, Affonso Rocha - Curso de Desenho Geométrico. Ed. Nobel, São Paulo: 1954 OCLC 819663445.
  • Mandarino, Denis - Desenho Geométrico, construções com régua e compasso. Ed. Plêiade, São Paulo: 2007 ISBN 978-85-7651-045-1 Livro.
  • Marmo, Carlos - Desenho Geométrico. Ed. Scipione, São Paulo: 1995 ISBN 85-262-2192-2 e ISBN 85-262-2190-6 .
  • Putnoki, José Carlos - Elementos de geometria e desenho geométrico. Vol. 1 e 2. Ed. Scipione, São Paulo: 1990 ISBN 8-526-21467-5 .

Ligações externas

  • Venturi, Jacir J. (2003). Cônicas e Quádricas (PDF) 5 ed. Curitiba: Unificado. 246 páginas. ISBN 8585132485 
  • Animação 3D de um plano seccionando um cone e definindo a curva cônica elipse
  • «Construir objetos geometria analítica» (em inglês) 
  • Alfred North Whitehead: An Introduction to Mathematics. BiblioBazaar LLC 2009 (reprint), ISBN 9781103197842, pp. 121 [1]
  • George Wentworth: Junior High School Mathematics: Book III. BiblioBazaar LLC 2009 (reprint), ISBN 9781103152360, pp. 265 [2]
  • Robert Clarke James, Glenn James: Mathematics Dictionary. Springer 1992, ISBN 9780412990410, p. 255 [3]
Ícone de esboço Este artigo sobre astronomia é um esboço. Você pode ajudar a Wikipédia expandindo-o.
  • v
  • d
  • e
  • Portal da astronomia
  • Portal da matemática
Controle de autoridade