Epicicloide

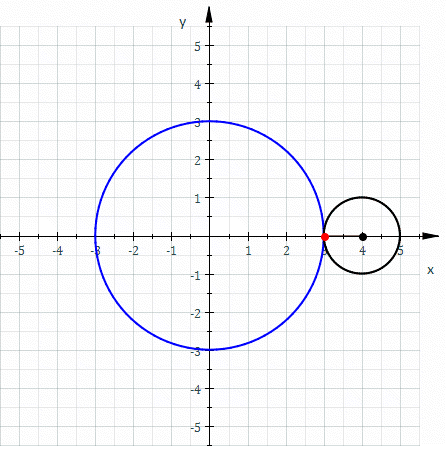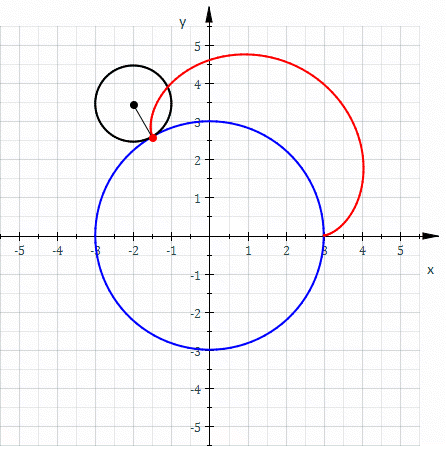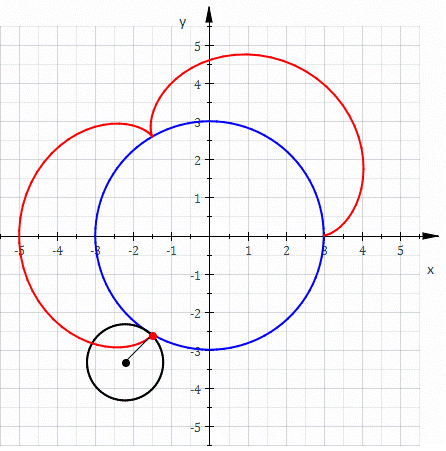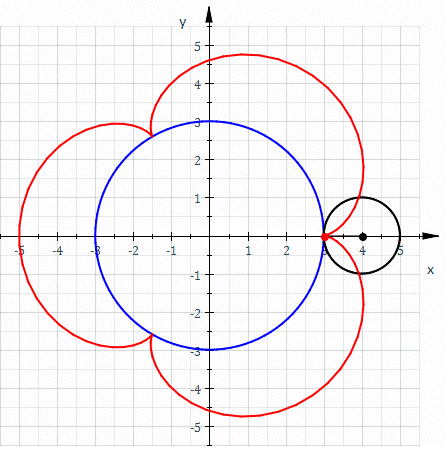
A epicicloide é uma curva cíclica definida por um ponto de uma circunferência que rola sem deslizar sobre um círculo diretor^[1]. A epicicloide é um caso especial da epitrocoide. Uma epicicloide com um único ponto tangendo a circunferência é uma cardioide.

História

O matemático grego Hiparco (190 aC - 120 aC) foi o primeiro a desenvolver as ideias de epicicloide em sua teoria astronômica dos epiciclos, onde desenvolveu um modelo para o movimento lunar. Em seguida, Ptolemeu, famoso astrônomo e geógrafo grego, usou combinações de epicicloides para estimar as posições do Sol, da Lua e dos planetas. Essa ideia só foi substituída pela teoria de Nicolau Copérnico (1473 - 1543) de que o Sol, e não a Terra, era o centro do universo.

A construção em si da epicicloide foi primeiramente descrita em 1525 por Albrecht Dürer (1471 - 1528), um artista alemão. Dürer publicou essa e muitas outras curvas em seu primeiro artigo matemático. Gerard Desargues (1591 - 1661), engenheiro francês, foi o primeiro a fazer uso da epicicloide nos sistemas de abastecimento de água na região de Paris. Outro uso prático da epicicloide é o da engrenagem mecânica, ainda que se debata de quem foi a ideia. Olaus Roemer (1644 - 1710), astrônomo dinamarquês, é tido como o autor da investigação do uso da epicicloide nos dentes das engrenagens apesar de haver uma discussão envolvendo o matemático francês Philippe de La Hire (1640 - 1719) cujo pai foi aluno de Desargues, que supostamente teria feito o mesmo vinte anos antes.

Demonstração

Assumimos que a posição do ponto ${\displaystyle p}$ é o que queremos solucionar, ${\displaystyle \alpha }$ é o ângulo em radiano a partir do ponto tangenciado até o ponto móvel ${\displaystyle p}$, e ${\displaystyle \theta }$ é o ângulo em radiano a partir do ponto inicial até o ponto tangenciado.

Como não há deslizamento entre os dois círculos,

${\displaystyle \ell _{R}=\ell _{r}}$

A partir da definição de radiano (tamanho do arco sobre o raio), temos que

${\displaystyle \ell _{R}=\theta R,\ell _{r}=\alpha r}$

A partir dessas duas condições, temos

${\displaystyle \theta R=\alpha r}$

Assim,

${\displaystyle \alpha ={\frac {R}{r}}\theta }$

Observando a figura, vemos facilmente a posição do ponto ${\displaystyle p}$.

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left(\theta +\alpha \right)=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\sin \theta -r\sin \left(\theta +\alpha \right)=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right)}$

Involuta

A involuta de uma epicicloide parametrizada da forma

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\operatorname {sen} \theta -r\operatorname {sen} \left({\frac {R+r}{r}}\theta \right)}$

é outra epicicloide dada por

${\displaystyle x=\left({\frac {R+2r}{r}}\right)\left[\left(R+r\right)\cos \theta +r\cos \left[\left({\dfrac {R+r}{r}}\right)\theta \right]\right]}$

${\displaystyle y=\left({\frac {R+2r}{r}}\right)\left[\left(R+r\right)\operatorname {sen} \theta +r\operatorname {sen} \left[\left({\dfrac {R+r}{r}}\right)\theta \right]\right]}$

representada pela cor azul na figura ao lado, com R = 3 e r = 1.

Evoluta

A evoluta de uma epicicloide parametrizada da forma

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\operatorname {sen} \theta -r\operatorname {sen} \left({\frac {R+r}{r}}\theta \right)}$

é outra epicicloide dada por

${\displaystyle x=\left({\frac {r}{R+2r}}\right)\left[\left(R+r\right)\cos \theta +r\cos \left[\left({\dfrac {R+r}{r}}\right)\theta \right]\right]}$

${\displaystyle x=\left({\frac {r}{R+2r}}\right)\left[\left(R+r\right)\operatorname {sen} \theta +r\operatorname {sen} \left[\left({\dfrac {R+r}{r}}\right)\theta \right]\right]}$

representada pela cor verde na figura ao lado, com R = 5 e r = 1.

Epicicloide encurtada

Se o ponto da curva estiver dentro da circunferência, a curva descrita será uma epicicloide encurtada^[2].

Epicicloide alongada

Se o ponto da curva estiver fora da circunferência, a curva descrita será uma epicicloide alongada.^[2]

Galeria de epicicloides

• Exemplos de epicicloides
• 
  k = 1
• 
  k = 2
• 
  k = 3
• 
  k = 4
• 
  k = 2.1 = 21/10
• 
  k = 3.8 = 19/5
• 
  k = 5.5 = 11/2
• 
  k = 7.2 = 36/5

Ver também

• Lista de construções do desenho geométrico

Referências

Ligações externas

• Animação da cicloide, epicicloide, hipocicloide
• Curvas Cíclicas
• The Epicycloid by Dennis Astley e Emily Astley (em inglês).