Diferencijalni račun

Grafikon funkcije, nacrtan u crnom bojom, i tangenta te funkciju, nacrtana crvenom bojom. Nagib tangentne linije jednak je derivatu funkcije na označenoj tački.

U matematici, diferencijalni račun je podpolje računa[1] koje se bavi proučavanjem stopa kojima se veličine menjaju. To je jedan od dva tradicionalna dela računa, pri čemu je drugi integralni račun, proučavanje područja ispod krive.[2]

Primarni predmeti proučavanja u diferencijalnom računu su derivacija funkcije, srodni pojmovi kao što su diferencijali i njihove primene. Derivat funkcije pri izabranoj ulaznoj vrednosti opisuje brzinu promene funkcije u blizini te ulazne vrednosti. Proces pronalaženja derivata se naziva diferencijacija. Geometrijski, derivat u tački je nagib tangentne linije na grafikonu funkcije u toj tački, pod uslovom da derivat postoji i da je definisan u toj tački. Za funkciju realnih vrednosti jedne realne promenljive, derivat funkcije u tački generalno određuje najbolju linearnu aproksimaciju funkcije u toj tački. Diferencijalni račun i integralni račun su povezani fundamentalnim teoremom računa, koji navodi da je diferencijacija obrnuti proces integracije.

Diferencijacija nalazi primene u skoro svim kvantitativnim disciplinama. Na primer, u fizici, derivat pomeranja pokretnog tela u odnosu na vreme je brzina tela, a derivat brzine u odnosu na vreme je ubrzanje. Derivat momenta tela u odnosu na vreme jednak je sili primenjenoj na telo; preraspodela izraza ovog derivata dovodi do poznate jednačine F = ma, povezane sa Njutnovim drugim zakonom kretanja. Brzina hemijske reakcije je derivat. U operacionim istraživanjima, derivati određuju najefikasnije načine za transport materijala i dizajniranje fabrika.

Derivati se često koriste za pronalaženje maksimuma i minimuma funkcije. Jednačine koje uključuju derivate nazivaju se diferencijalne jednačine i fundamentalne su za opisivanje prirodnih fenomena. Derivati i njihove generalizacije pojavljuju se u mnogim oblastima matematike, kao što su kompleksna analiza, funkcionalna analiza, diferencijalna geometrija, teorija mera i apstraktna algebra.

Izvod

Tangetna linija u (x,f(x))
Izvod raznih tačaka diferencijabilne funkcije

Pretpostavimo da su x i y realni brojevi i da je y funkcija od x, to jest, za svaku vrednost x postoji odgovarajuća vrijednost y. Ovaj odnos se može zapisati kao y = f(x). Ako je f(x) jednačina za pravu liniju (zvana linearna jednačina), onda postoje dva realna broja m i b takva da je y = mx + b. U ovoj „formi nagiva i preseka”, izraz m se naziva nagib i može se odrediti iz formule:

m = promena u  y promena u  x = Δ y Δ x , {\displaystyle m={\frac {{\text{promena u }}y}{{\text{promena u }}x}}={\frac {\Delta y}{\Delta x}},}

gde je simbol Δ (veliko grčko slovo delta) skraćenica za „promena u”. Odatle sledi da je Δy = m Δx.

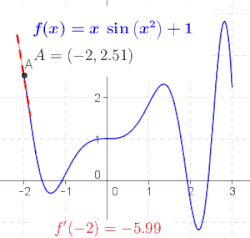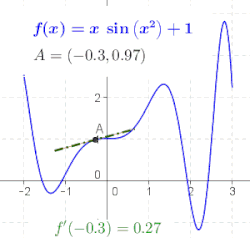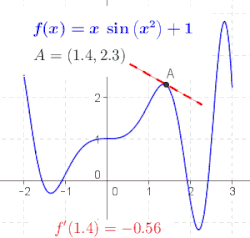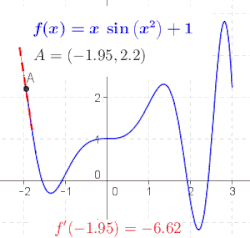
Generalna funkcija nije linija, tako da nema nagib. Geometrijski, izvod od f u tački x = a je nagib tangentne linije funkcije f u tački a (pogledajte sliku). To se često označava sa f ′(a) u Lagranžovoj notaciji ili dy/dx|x = a u Lajbnicovoj notaciji. Kako je izvod nagib linearne aproksimacije od f u tački a, izvod (zajedno sa vrednošću f u a) određuje najbolju linearnu aproksimaciju, ili linearizaciju, od f u blizini tačkie a.

Ako svaka tačka a u domenu funkcije f ima izvod, onda postoji funkcija koja šalje svaku tačku a u derivat od f u a. Na primer, ako je f(x) = x2, onda je funkcija izvoda f ′(x) = dy/dx = 2x.

Blisko srodna notacije je diferencijal funkcije.[3][4] Kad su x i y realne promenljive, derivat f od x je nagib tangetne linije na grafikonu f od x. Budući da su izvor i cilj funkcije f jednodimenzionalni, derivat od f je realni broj. Ako su x i y vektori, tada najbolja linearna aproksimacija grafu f zavisi od toga kako se f menja u više smerova odjednom. Uzimajući najbolju linearnu aproksimaciju u jednom pravcu, određuje se parcijalni derivat, koji se obično označava ∂y/∂x. Linearizacija f u svim pravcima odjednom se naziva totalni derivat.[5]

Reference

  1. ^ „Definition of differential calculus”. www.merriam-webster.com (на језику: енглески). Приступљено 2018-09-26. 
  2. ^ „"Integral Calculus - Definition of Integral calculus by Merriam-Webster"”. www.merriam-webster.com (на језику: енглески). Приступљено 2018-05-01. 
  3. ^ „Differential”. Wolfram MathWorld. Приступљено 24. 2. 2022. „The word differential has several related meaning in mathematics. In the most common context, it means "related to derivatives." So, for example, the portion of calculus dealing with taking derivatives (i.e., differentiation), is known as differential calculus.
    The word "differential" also has a more technical meaning in the theory of differential k-forms as a so-called one-form.    ”     CS1 одржавање: Формат датума (веза)
  4. ^ „differential - Definition of differential in US English by Oxford Dictionaries”. Oxford Dictionaries - English. Архивирано из оригинала 3. 1. 2014. г. Приступљено 13. 4. 2018. CS1 одржавање: Формат датума (веза)
  5. ^ „Math 150B Exam 3 Solution | California State University - KeepNotes”. keepnotes.com. Приступљено 2023-09-27. 

Literatura

  • J. Edwards (1892). Differential Calculus. London: MacMillan and Co. 
  • Larson, Ron, Bruce H. Edwards. "Calculus", 9th ed., Brooks Cole Cengage Learning. 2010. ISBN 978-0-547-16702-2..
  • McQuarrie, Donald A (2003). Mathematical Methods for Scientists and Engineers. University Science Books. ISBN 978-1-891389-24-5. 
  • Stewart, James (2008). Calculus: Early Transcendentals. 6th ed., Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8. 
  • Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano.. "Calculus", 11th ed., Addison-Wesley. 2008. ISBN 0-321-48987-X..
  • Courant, Richard. ISBN 978-3-540-65058-4. Introduction to calculus and analysis 1.
  • Edmund Landau. ISBN 0-8218-2830-4 Differential and Integral Calculus, American Mathematical Society.
  • Robert A. Adams. 1999. ISBN 978-0-201-39607-2.. Calculus: A complete course.
  • Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.
  • John Lane Bell (1998). A Primer of Infinitesimal Analysis. Cambridge University Press. ISBN 978-0-521-62401-5.  Uses synthetic differential geometry and nilpotent infinitesimals.
  • Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46.
  • Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton University Press, 2004.
  • Cliff Pickover. 2003. ISBN 978-0-471-26987-8.. Calculus and Pizza: A Math Cookbook for the Hungry Mind.
  • Michael Spivak. (September 1994). ISBN 978-0-914098-89-8. Calculus. Publish or Perish publishing.
  • Tom M. Apostol. 1967. ISBN 978-0-471-00005-1.. Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.
  • Tom M. Apostol. 1969. ISBN 978-0-471-00007-5.. Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.
  • Silvanus P. Thompson and Martin Gardner. 1998. ISBN 978-0-312-18548-0.. Calculus Made Easy.
  • Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
  • Thomas/Finney. 1996. ISBN 978-0-201-53174-9.. Calculus and Analytic geometry 9th, Addison Wesley.
  • Weisstein, Eric W. "Second Fundamental Theorem of Calculus." From MathWorld—A Wolfram Web Resource.
  • Crowell, B. (2003). "Calculus" Light and Matter, Fullerton., Приступљено 6. 5. 2007. from http://www.lightandmatter.com/calc/calc.pdf
  • Garrett, P. (2006). "Notes on first year calculus" University of Minnesota., Приступљено 6. 5. 2007. from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
  • Faraz, H. (2006). "Understanding Calculus", Приступљено 6. 5. 2007. from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
  • Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals", Приступљено 29. 8. 2010. from http://www.math.wisc.edu/~keisler/calc.html
  • Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology., Приступљено 6. 5. 2007. from https://web.archive.org/web/20070614183657/http://www.cacr.caltech.edu/~sean/applied_math.pdf
  • Sloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus"., Приступљено 17. 3. 2009. from http://synechism.org/drupal/de2de/
  • Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa., Приступљено 6. 5. 2007. from https://web.archive.org/web/20050911104158/http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm (HTML only)
  • Strang, G. (1991). "Calculus" Massachusetts Institute of Technology., Приступљено 6. 5. 2007. from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm
  • Smith, William V. (2001). "The Calculus", Приступљено 4. 7. 2008. [1] (HTML only).
  • Roero, C.S. (2005). „Gottfried Wilhelm Leibniz, first three papers on the calculus (1684, 1686, 1693)”. Ур.: Grattan-Guinness, I. Landmark writings in Western mathematics 1640–1940. Elsevier. стр. 46—58. ISBN 978-0-444-50871-3. 
  • Roero, C.S. (1983). „Jakob Bernoulli, attentive student of the work of Archimedes: marginal notes to the edition of Barrow”. Boll. Storia Sci. Mat. 3 (1): 77—125. 
  • Boyer, Carl (1959). The History of the Calculus and its Conceptual Development. New York: Dover Publications.  Republication of a 1939 book (2nd printing in 1949) with a different title.
  • Calinger, Ronald (1999). A Contextual History of Mathematics. Toronto: Prentice-Hall. ISBN 978-0-02-318285-3. 
  • Reyes, Mitchell (2004). „The Rhetoric in Mathematics: Newton, Leibniz, the Calculus, and the Rhetorical Force of the Infinitesimal”. Quarterly Journal of Speech. 90 (2): 159—184. doi:10.1080/0033563042000227427. 
  • Grattan-Guinness, Ivor. The Rainbow of Mathematics: A History of the Mathematical Sciences, Chapters 5 and 6, W. W. Norton & Company, 2000.
  • Hoffman, Ruth Irene, "On the development and use of the concepts of the infinitesimal calculus before Newton and Leibniz", Thesis (M.A.), University of Colorado, 1937

Spoljašnje veze

Diferencijalni račun na Vikimedijinoj ostavi.
  • Hazewinkel Michiel, ур. (2001). „Calculus”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
  • Weisstein, Eric W. „Calculus”. MathWorld. 
  • Topics on Calculus at PlanetMath.org.
  • Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
  • Calculus on In Our Time at the BBC. (listen now)
  • Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
  • COW: Calculus on the Web Архивирано на сајту Wayback Machine (8. април 2011) at Temple University – contains resources ranging from pre-calculus and associated algebra
  • Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
  • Online Integrator (WebMathematica) from Wolfram Research
  • The Role of Calculus in College Mathematics Архивирано на сајту Wayback Machine (26. јул 2021) from ERICDigests.org
  • OpenCourseWare Calculus Архивирано на сајту Wayback Machine (5. мај 2010) from the Massachusetts Institute of Technology
  • Infinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, ed. Michiel Hazewinkel.
  • Daniel Kleitman, MIT. „Calculus for Beginners and Artists”. 
  • Calculus Problems and Solutions by D.A. Kouba
  • Donald Allen's notes on calculus Архивирано на сајту Wayback Machine (23. март 2021)
  • Calculus training materials at imomath.com
Normativna kontrola: Državne Уреди на Википодацима
  • Nemačka
  • Izrael
  • Češka