Trójki pitagorejskie

Trójka pitagorejska (albo liczby pitagorejskie^[1]) – trzy liczby całkowite dodatnie ${\displaystyle a,b,c}$ spełniające tzw. równanie Pitagorasa:

${\displaystyle a^{2}+b^{2}=c^{2}.}$

Ich nazwa pochodzi od twierdzenia Pitagorasa, na mocy którego boki trójkąta prostokątnego spełniają powyższą zależność. W poniższej tabeli przedstawiono kilka pierwszych (względem krótszej przyprostokątnej) trójek pitagorejskich:

${\displaystyle a}$	${\displaystyle b}$	${\displaystyle c}$
3	4	5
5	12	13
6	8	10
7	24	25
8	15	17
9	12	15
10	24	26
12	16	20

Własności

Jeżeli trójka ${\displaystyle (a,b,c)}$ jest pitagorejska, to jest nią też ${\displaystyle (da,db,dc),}$ dla dowolnej liczby całkowitej dodatniej ${\displaystyle d.}$ Trójkę pitagorejską nazywamy pierwotną, jeśli ${\displaystyle a,}$ ${\displaystyle b}$ i ${\displaystyle c}$ nie mają wspólnego dzielnika większego od 1. Zatem z każdej trójki pitagorejskiej możemy uzyskać pierwotną przez podzielenie jej przez największy wspólny dzielnik i dowolną trójkę pitagorejską możemy otrzymać z pierwotnej przez pomnożenie jej wszystkich trzech elementów przez odpowiednią tę samą liczbę całkowitą dodatnią.

Jeśli ${\displaystyle m>n}$ są liczbami całkowitymi dodatnimi, to

${\displaystyle a=m^{2}-n^{2},}$

${\displaystyle b=2\cdot m\cdot n,}$

${\displaystyle c=m^{2}+n^{2}}$

jest trójką pitagorejską. Jest ona pierwotna wtedy i tylko wtedy, gdy ${\displaystyle m}$ i ${\displaystyle n}$ są względnie pierwsze i ich suma jest liczbą nieparzystą. Trójki pitagorejskiej (9, 12, 15), jak również wielu innych, w ten sposób nie otrzymamy, ale każda trójka pierwotna (być może po zamianie ${\displaystyle a}$ i ${\displaystyle b}$) powstaje tą drogą z jedynej pary liczb względnie pierwszych ${\displaystyle m>n.}$ Stąd wniosek, że istnieje nieskończenie wiele pierwotnych trójek pitagorejskich.

Trójkąt, którego długości boków stanowią trójkę pitagorejską, nazywany jest trójkątem pitagorejskim. Z kolei trójkąt o bokach długości 3, 4 i 5 nazywa się trójkątem egipskim.

Rozwiązanie elementarne

Kwadrat nieparzystej liczby naturalnej przy dzieleniu przez 8 daje resztę 1. Zatem suma kwadratów dwóch dowolnych liczb nieparzystych daje resztę 2 z dzielenia przez 8. Z drugiej strony, kwadrat dowolnej liczby naturalnej daje przy dzieleniu przez 8 jedną z reszt 0, 1, 4. Zatem suma dwóch kwadratów nieparzystych liczb naturalnych nigdy nie jest kwadratem.

Niech ${\displaystyle a,b,c}$ będą liczbami naturalnymi, spełniającymi równanie:

${\displaystyle a^{2}+b^{2}=c^{2}.}$

(1)

Zatem co najmniej jedna z liczb ${\displaystyle a,b,}$ jest parzysta. Przy założeniu, że ${\displaystyle a,b,}$ są względnie pierwsze, jedna z liczb ${\displaystyle a,b,}$ powiedzmy ${\displaystyle a,}$ jest nieparzysta, a ${\displaystyle b}$ jest parzysta. Zatem ${\displaystyle c}$ jest nieparzysta i względnie pierwsza zarówno z liczbą ${\displaystyle a,}$ jak i z liczbą ${\displaystyle b.}$

Każdy wspólny dzielnik liczb naturalnych ${\displaystyle (c-a)/2}$ oraz ${\displaystyle (c+a)/2}$ jest też dzielnikiem ich sumy, równej ${\displaystyle c,}$ oraz ich różnicy, równej ${\displaystyle a,}$ jest więc równy 1, a liczby ${\displaystyle (c-a)/2}$ oraz ${\displaystyle (c+a)/2}$ są względnie pierwsze.

Równanie (1) ma dokładnie te same rozwiązania ${\displaystyle (a,b,c),}$ co równanie:

${\displaystyle {\frac {c-a}{2}}\cdot {\frac {c+a}{2}}=\left({\frac {b}{2}}\right)^{2}.}$

(2)

Ponieważ liczby ${\displaystyle (c-a)/2}$ oraz ${\displaystyle (c+a)/2}$ są względnie pierwsze, to są pełnymi kwadratami pewnych liczb naturalnych ${\displaystyle m}$ oraz ${\displaystyle n{:}}$

${\displaystyle {\frac {c+a}{2}}=m^{2},}$

${\displaystyle {\frac {c-a}{2}}=n^{2},}$

skąd:

${\displaystyle a=m^{2}-n^{2},}$

${\displaystyle b=2\cdot m\cdot n,}$

${\displaystyle c=m^{2}+n^{2}.}$

Dla każdego pierwotnego rozwiązania ${\displaystyle (a,b,c)}$ równania (1) istnieją liczby naturalne ${\displaystyle m}$ oraz ${\displaystyle n,}$ takie że rozwiązanie ${\displaystyle (a,b,c)}$ wyraża się poprzez ${\displaystyle m}$ oraz ${\displaystyle n}$ jak wyżej. Aby otrzymać rozwiązanie pierwotne, należy wybrać liczby ${\displaystyle m}$ oraz ${\displaystyle n}$ o różnej parzystości i względnie pierwsze. Ostatnie trzy równości posłużą wtedy za definicję rozwiązania.

Wariacja

W poprzednim fragmencie, i wciąż uznając jego założenia, zamiast równania (2), rozpatrzmy równanie

${\displaystyle (c-b)\cdot (c+b)=a^{2}.}$

(3)

Każdy wspólny dzielnik nieparzystych liczb ${\displaystyle c-b}$ oraz ${\displaystyle c+b}$ jest też wspólnym dzielnikiem ich sumy, równej ${\displaystyle 2\cdot c,}$ oraz różnicy, równej ${\displaystyle 2\cdot b,}$ czyli jest równy 1 lub 2 (mówimy tylko o dodatnich liczbach całkowitych; w dalszym ciągu obowiązuje założenie z poprzedniego fragmentu o względnej pierwszości liczb ${\displaystyle a,b,}$ a więc i liczb ${\displaystyle b,c}$). Ale 2 nie jest podzielnikiem nieparzystych liczb ${\displaystyle c-b}$ oraz ${\displaystyle c+b.}$ Zatem są one względem pierwsze; więc są odpowiednio kwadratami pewnych nieparzystych, dodatnich liczb całkowitych ${\displaystyle x,y,}$ czyli:

${\displaystyle a=x\cdot y,}$

${\displaystyle b={\frac {y^{2}-x^{2}}{2}},}$

${\displaystyle c={\frac {x^{2}+y^{2}}{2}}.}$

Wykazano tu, że dla każdego rozwiązania pierwotnego ${\displaystyle (a,b,c)}$ istnieją nieparzyste dodatnie liczby całkowite ${\displaystyle x}$ oraz ${\displaystyle y,}$ takie, że rozwiązanie ${\displaystyle (a,b,c)}$ określone jest przez powyższe trzy równości. Tak zadane przez nieparzyste ${\displaystyle x}$ oraz ${\displaystyle y}$ rozwiązanie ${\displaystyle (a,b,c)}$ jest pierwotne wtedy i tylko wtedy, gdy ${\displaystyle x,y}$ są względnie pierwsze.

Otrzymaliśmy nową parametryzację pierwotnych trójek pitagorejskich, nieco różną od poprzedniej.

Ogólnie, gdy liczby ${\displaystyle x,y}$ są tej samej parzystości, to powyższa trójka równości definiuje pewną trójkę pitagorejską, niekoniecznie pierwotną. Nie otrzyma się w ten sposób trójki pitagorejskiej (6, 8, 10) i wielu innych.

Wariacja II

Na podstawie metody przyrostów kwadratów liczb parzystych i nieparzystych można wyprowadzić zależność:

${\displaystyle (a+t)^{2}=a^{2}+b^{2},}$

${\displaystyle c=a+t,}$

${\displaystyle a={\frac {b^{2}-t^{2}}{2t}}.}$

W powyższej zależności ${\displaystyle t}$ jest dzielnikiem ${\displaystyle b}$ takim, że dla parzystego ${\displaystyle b}$ parametr ${\displaystyle t}$ jest również parzysty, a dla nieparzystego ${\displaystyle b}$ jest nieparzysty. Dla wartości parametru ${\displaystyle t=1}$ i ${\displaystyle t=2}$ (z wyjątkiem liczb typu ${\displaystyle 2\cdot p}$) otrzymujemy trójki pierwotne. Dla pozostałych dzielników ${\displaystyle t}$ tworzone są pozostałe i możliwe kombinacje trójek pitagorejskich dla zadanego ${\displaystyle b.}$

Dla ${\displaystyle t=1}$ i ${\displaystyle k>0}$ zależność jest następująca:

${\displaystyle a=2k(k+1),}$

${\displaystyle b=2k+1,}$

${\displaystyle c=2k(k+1)+1.}$

Dla ${\displaystyle t=2}$ i ${\displaystyle k>0}$ zależność jest następująca:

${\displaystyle a=k(k+2),}$

${\displaystyle b=2k+2,}$

${\displaystyle c=k(k+2)+2.}$

co łatwo udowodnić, podstawiając za ${\displaystyle a,}$ ${\displaystyle b}$ i ${\displaystyle c}$ ogólne wyrażenia. Nie otrzyma się w ten sposób np. trójki ${\displaystyle (88,105,137)}$ i wielu innych.

Rozwiązanie zespolone z użyciem liczb Gaussa

Niech ${\displaystyle i}$ oznacza jedną z dwóch liczb zespolonych, których kwadrat jest równy ${\displaystyle -1{:}}$

${\displaystyle i^{2}=-1.}$

Liczby postaci ${\displaystyle a+i\cdot b,}$ gdzie ${\displaystyle a}$ oraz ${\displaystyle b}$ są liczbami całkowitymi, nazywamy liczbami Gaussa. Tworzą one pierścień Gaussa. W pierścieniu Gaussa istnieją dokładnie cztery jedności, czyli liczby multiplikatywnie odwracalne:

${\displaystyle 1,i,-1,-i.}$

(Liczbę 1 nazywamy jedynką). Liczba sprzężona do jedności ${\displaystyle u}$ jest jej odwrotnością ${\displaystyle 1/u.}$

Liczbę Gaussa nazywa się liczbą pierwszą, gdy w każdym jej rozkładzie na iloczyn dwóch liczb Gaussa jeden z czynników jest jednością. Iloczyn liczby pierwszej Gaussa przez jedność też jest liczbą pierwszą. Tak związane pary liczb pierwszych nazywamy liczbami równoważnymi. Każda różna od zera liczba Gaussa rozkłada się na skończony iloczyn liczb pierwszych Gaussa, jednoznacznie z dokładnością do równoważności i kolejności występowania w iloczynie.

Gdy liczba Gaussa ${\displaystyle z}$ jest iloczynem liczb Gaussa ${\displaystyle x}$ oraz ${\displaystyle y,}$ to liczby ${\displaystyle x}$ oraz ${\displaystyle y}$ nazywamy dzielnikami liczby ${\displaystyle z}$ (w pierścieniu Gaussa). Gdy ${\displaystyle z}$ jest liczbą rzeczywistą (gdy ma część urojoną równą zero), to dzielnikami są także liczby Gaussa sprzężone bowiem ogólnie:

${\displaystyle z=(a+i\cdot b)\cdot (c+i\cdot d)\;\Leftrightarrow \;z=(a-i\cdot b)\cdot (c-i\cdot d),}$

gdy ${\displaystyle a,b,c,d,z\in \mathbb {R} .}$

Dwie liczby Gaussa nazywamy względnie pierwszymi, gdy ich jedynymi wspólnymi podzielnikami są jedności. (Tak więc jedności i tylko jedności są względnie pierwsze z dowolną liczbą Gaussa). Dwie liczby naturalne są względnie pierwsze w klasycznym sensie (w kontekście ciała liczb wymiernych) wtedy i tylko wtedy gdy są względnie pierwsze jako liczby Gaussa (w pierścieniu liczb Gaussa).

Powróćmy teraz do równania:

${\displaystyle a^{2}+b^{2}=c^{2},}$

(1)

gdzie ${\displaystyle a,b,}$ oznaczają względnie pierwsze, dodatnie liczby całkowite. Zapiszmy równanie (1) równoważnie:

${\displaystyle (a-i\cdot b)\cdot (a+i\cdot b)=c^{2}.}$

(1G)

Każdy dzielnik liczb ${\displaystyle a-i\cdot b}$ oraz ${\displaystyle a+i\cdot b}$ jest też dzielnikiem ich sumy ${\displaystyle 2\cdot a}$ oraz różnicy ${\displaystyle 2\cdot i\cdot b,}$ a więc liczby 2. Zakładając, jak we wcześniejszych fragmentach, że ${\displaystyle (a,b,c)}$ jest rozwiązaniem pierwotnym, liczby ${\displaystyle a}$ oraz ${\displaystyle b}$ są ponadto różnej parzystości, więc ${\displaystyle a-i\cdot b}$ oraz ${\displaystyle a+i\cdot b}$ są względnie pierwsze. Skoro tak, to są one kwadratami liczb Gaussa, pomnożonymi przez jedność, to znaczy: istnieją liczby całkowite (wymierne) ${\displaystyle X}$ oraz ${\displaystyle Y,}$ oraz jedność gaussowska ${\displaystyle u}$ (równa ${\displaystyle 1}$ lub ${\displaystyle i}$ lub ${\displaystyle -1}$ lub ${\displaystyle -i}$), dla których:

${\displaystyle a+i\cdot b=(x+i\cdot Y)^{2}\cdot u,}$

${\displaystyle a-i\cdot b=(x-i\cdot Y)^{2}/u.}$

Drugie równanie wynika z pierwszego. Wystarczy rozpatrywać przypadki ${\displaystyle u=1}$ oraz ${\displaystyle u=i,}$ jako że ${\displaystyle -1=i^{2}}$ oraz ${\displaystyle -i=i\cdot i^{2}.}$ Dla ${\displaystyle u=1}$ otrzymujemy:

${\displaystyle a=X^{2}-Y^{2},}$

${\displaystyle b=2\cdot X\cdot Y=2\cdot |X|\cdot |Y|,}$

${\displaystyle c=X^{2}+Y^{2}.}$

Gdy ${\displaystyle u=i,}$ to otrzymujemy:

${\displaystyle b+i\cdot a=(X-i\cdot Y)^{2},}$

skąd:

${\displaystyle a=-2\cdot X\cdot Y=2\cdot |X|\cdot |Y|,}$

${\displaystyle b=X^{2}-Y^{2},}$

${\displaystyle c=X^{2}+Y^{2}.}$

Wprowadźmy liczby ${\displaystyle x:=|X|}$ oraz ${\displaystyle y:=|Y|.}$ Oczywiście ${\displaystyle x\neq 0\neq y.}$ Pokazaliśmy, że dla dowolnego rozwiązania pierwotnego ${\displaystyle (a,b,c)}$ równania (1) istnieją całkowite liczby dodatnie ${\displaystyle x}$ oraz ${\displaystyle y}$ (wymierne), takie że odpowiednio:

${\displaystyle a=x^{2}-y^{2}\quad {}}$ lub ${\displaystyle {}\quad a=2\cdot x\cdot y,}$

${\displaystyle b=x^{2}-y^{2}\quad {}}$ lub ${\displaystyle {}\quad b=2\cdot x\cdot y,}$

${\displaystyle c=x^{2}+y^{2}.}$

Rozwiązanie geometryczne

Można prosto rozwiązać równanie^[2]

${\displaystyle a^{2}+b^{2}=c^{2},}$

(1)

korzystając z narzędzi elementarnej geometrii algebraicznej. Z rozwiązań wymiernych ${\displaystyle (a,b,c)}$ tego równania otrzymujemy rozwiązania całkowite, mnożąc liczby wymierne ${\displaystyle a,b,c}$ przez ich wspólny mianownik. Zauważmy ponadto, że jeśli ${\displaystyle c=0,}$ to jedynym rozwiązaniem równania

${\displaystyle a^{2}+b^{2}=c^{2}}$

jest trójka liczb (0, 0, 0). Rozwiązanie to będziemy nazywać rozwiązaniem zerowym.

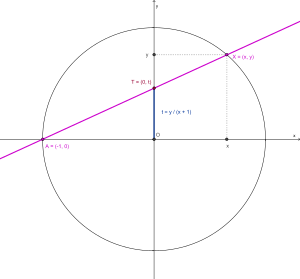
Każdemu niezerowemu rozwiązaniu całkowitemu ${\displaystyle (a,b,c)}$ odpowiada rozwiązanie

${\displaystyle x={\frac {a}{c}},\ y={\frac {b}{c}}}$

równania:

${\displaystyle x^{2}+y^{2}=1.}$

(4)

Jest to równanie okręgu jednostkowego o środku w początku układu współrzędnych. Również każdemu rozwiązaniu wymiernemu ${\displaystyle (x,y)}$ równania ${\displaystyle x^{2}+y^{2}=1}$ odpowiadają takie rozwiązania całkowite ${\displaystyle (a,b,c)}$ równania Pitagorasa, że ${\displaystyle a=xc,\ b=yc}$ (wystarczy, aby liczba ${\displaystyle c}$ była podzielna przez mianowniki liczb ${\displaystyle x}$ i ${\displaystyle y}$). Aby rozwiązać równanie Pitagorasa, wystarczy znaleźć punkty na okręgu jednostkowym o obu współrzędnych wymiernych. Jednym z rozwiązań jest ${\displaystyle (x_{0},y_{0})=(-1,0).}$ Przez ten punkt oraz dowolny inny wymierny punkt okręgu możemy poprowadzić prostą. Współczynnik kierunkowy ${\displaystyle t}$ tej prostej jest liczbą wymierną. Dlatego ten drugi punkt jest rozwiązaniem układu równań (4) i (5):

${\displaystyle y=t\cdot (x+1)}$

(5)

dla pewnej liczby wymiernej ${\displaystyle t.}$ Trzeba wykazać, że dla dowolnej liczby wymiernej ${\displaystyle t}$ rozwiązanie powyższego układu jest liczbą wymierną. Po podstawieniu (5) do (4) dla ${\displaystyle x\neq -1}$ z (5) wynika, że:

${\displaystyle x^{2}+t^{2}\cdot (1+x)^{2}=1,}$

${\displaystyle t^{2}\cdot (1+x)^{2}=(1-x)(1+x),}$

${\displaystyle t^{2}(1+x)=1-x}$

(bo ${\displaystyle x\neq -1}$), skąd:

${\displaystyle x={\frac {1-t^{2}}{1+t^{2}}}.}$

Podstawiając obliczoną wartość ${\displaystyle x}$ do równania (5), otrzymujemy

${\displaystyle y={\frac {2\cdot t}{1+t^{2}}}.}$

W ten sposób wszystkie rozwiązania wymierne równania (4) wyrażone są za pomocą wymiernego parametru ${\displaystyle t.}$ Otrzymaliśmy tożsamość:

${\displaystyle \left({\frac {1-t^{2}}{1+t^{2}}}\right)^{2}+\left({\frac {2\cdot t}{1+t^{2}}}\right)^{2}=1}$

lub równoważnie:

${\displaystyle (1-t^{2})^{2}+(2\cdot t)^{2}=(1+t^{2})^{2}.}$

Po podstawieniu ${\displaystyle t:={\tfrac {n}{m}},}$ gdzie ${\displaystyle m}$ i ${\displaystyle n}$ są liczbami całkowitymi względnie pierwszymi ${\displaystyle (m\neq 0)}$ i pomnożeniu równania przez ${\displaystyle m^{4}{:}}$

${\displaystyle (m^{2}-n^{2})^{2}+(2\cdot m\cdot n)^{2}=(m^{2}+n^{2})^{2}.}$

Wtedy każde rozwiązanie całkowite równania (1) w liczbach ${\displaystyle a,b,c}$ względnie pierwszych wyraża się wzorami:

${\displaystyle a:=m^{2}-n^{2},}$

${\displaystyle b:=2\cdot m\cdot n,}$

${\displaystyle c:=m^{2}+n^{2}.}$

Liczby całkowite ${\displaystyle m>n>0}$ definiują rozwiązania całkowite dodatnie równania (1).

Konstrukcja z małego twierdzenie Fermata

Podejrzewając, że Fermat odkrył twierdzenie małe jako lemat by w prosty sposób udowodnić twierdzenie wielkie liczby pitagorejskie można konstruować bezpośrednio z małego twierdzenia Fermata działającego w jego najprostszej formie, tzn. dla liczby pierwszej ${\displaystyle 2}$ postępując tak jak byśmy chcieli z niego udowodnić twierdzenie wielkie.

Przepiszmy równanie Pitagorasa tak abyśmy mogli go bezpośrednio zastosować

${\displaystyle a^{2}-a+b^{2}-b=c^{2}-c+c-a-b.}$

Używając stronami twierdzenia małego otrzymujemy warunek że ${\displaystyle c-a-b}$ musi być podzielne przez ${\displaystyle 2}$ tzn.

${\displaystyle c=a+b-2k.}$

Wstawiając równanie na ${\displaystyle c}$ do równania Pitagorasa otrzymujemy równanie na ${\displaystyle a}$ względem ${\displaystyle b}$ i ${\displaystyle k}$

${\displaystyle a={\frac {2k(b-k)}{b-2k}},}$

które generuje razem z równaniem na ${\displaystyle c}$ trójki pitagorejskie w przypadku kiedy otrzymane ${\displaystyle a}$ jest całkowite. Teraz możemy pozbyć się tego defektu wstawiając uzyskane tak rozwiązania do oryginalnego równania i mnożąc przez mianownik w rozwiązaniu na a ${\displaystyle (b-2k)}$ w kwadracie.

Otrzymujemy w ten sposób tożsamość

${\displaystyle \left[2k(b-k)\right]^{2}+b^{2}(b-2k)^{2}=\left[2k(b-k)+(b-2k)^{2}\right]^{2}}$

wyrażającą sumę kwadratów dwóch liczb w funkcji dwóch parametrów jako kwadrat liczby w funkcji tych samych parametrów, tzn. zrenormalizowane liczby pitagorejskie wyrażone względem dowolnych naturalnych liczb ${\displaystyle b}$ i ${\displaystyle k{:}}$

${\displaystyle a_{1}=2k(b-k),}$

${\displaystyle b_{1}=b(b-2k),}$

${\displaystyle c_{1}=2k(b-k)+(b-2k)^{2},}$

spełniające równanie

${\displaystyle a_{1}^{2}+b_{1}^{2}=c_{1}^{2}.}$

W odróżnieniu od wyżej opisanych wzorów Euklidesa zawierających sumę kwadratów, różnicę kwadratów oraz podwójny iloczyn dwóch liczb ${\displaystyle m}$ i ${\displaystyle n,}$ wzory te dają wszystkie możliwe liczby pitagorejskie.

Dla ${\displaystyle k=4,}$ ${\displaystyle b=15}$ otrzymujemy np. ${\displaystyle a_{1}=88,}$ ${\displaystyle b_{1}=105,}$ ${\displaystyle c_{1}=137,}$ a dla ${\displaystyle k=1,}$ ${\displaystyle b=100000001,}$ ${\displaystyle a_{1}=200000000,}$ ${\displaystyle b_{1}=9999999999999999,}$ ${\displaystyle c_{1}=10000000000000001.}$

Warto zauważyć, że krok z użyciem małego twierdzenia Fermata, aby wyrazić ${\displaystyle c}$ względem ${\displaystyle a}$ i ${\displaystyle b}$ jako

${\displaystyle c=a+b-nk}$

dla dowolnego ${\displaystyle n>2}$ prowadzi do intuicyjnego pseudoudowodnienia twierdzenia wielkiego, ponieważ prowadzi do skomplikowanego równania algebraicznego ${\displaystyle n-1}$ rzędu na ${\displaystyle a}$ względem ${\displaystyle b,}$ ${\displaystyle k}$ zawierającego na dodatek liczbę pierwszą, wykładnik ${\displaystyle n}$ i już dla ${\displaystyle n=3}$ wydaje się mało prawdopodobne, by tak uzyskane równanie kwadratowe zawierające w rozwiązaniach pierwiastek kwadratowy miało rozwiązanie naturalne, nie mówiąc już o wzorach Cardana dla równania sześciennego czy równaniach wyższych niż stopnia czwartego, których ogólne rozwiązania nie dają się nawet wyrazić przez radykały, tzn. wyrażenia zawierające jedynie pierwiastki ${\displaystyle m}$-tego stopnia, które wszystkie na raz musiałyby być naturalne. Obecnie nawet wiadomo z istniejącego bardzo trudnego dowodu wielkiego twierdzenia Fermata, że jest to prawda, a liczby naturalne daje jedynie równanie liniowe na ${\displaystyle a}$ dla ${\displaystyle n=2.}$

Zobacz też

• małe twierdzenie Fermata

Przypisy

Linki zewnętrzne

• Tabela pierwotnych trójek pitagorejskich dla ${\displaystyle m,n\leqslant 300}$. [dostęp 2022-12-02]. [zarchiwizowane z tego adresu (2021-04-21)].
• Eric W.E.W. Weisstein Eric W.E.W., Pythagorean Triple, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-01].
• Eric W.E.W. Weisstein Eric W.E.W., Primitive Pythagorean Triple, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-01].