Coordenadas parabólicas

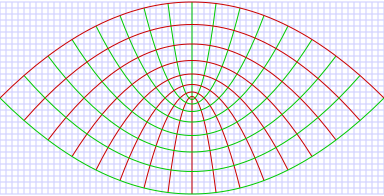
As coordenadas parabólicas são um sistema bidimensional de coordenadas ortogonais em que as linhas coordenadas são parábolas confocais. A versão tridimensional das coordenadas parabólicas é obtida através da rotação do sistema bidimensional sobre o eixo de simetria de todas as parábolas.

As coordenadas parabólicas possuem muitas aplicações, por exemplo, no tratamento do efeito Stark e da teoria potencial das arestas.

Coordenadas parabólicas bidimensionais

AS coordenadas parabólicas bidimensionais ( σ , τ ) {\displaystyle (\sigma ,\tau )} são definidas pelas equações

x = σ τ {\displaystyle x=\sigma \tau \,}
y = 1 2 ( τ 2 − σ 2 ) {\displaystyle y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}

As curvas com σ {\displaystyle \sigma } constante formam parábolas confocais

2 y = x 2 σ 2 − σ 2 {\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}

voltadas para cima (ou seja, no sentido + y {\displaystyle +y} ), ao passo que as curvas com τ {\displaystyle \tau } constante formam parábolas confocais

2 y = − x 2 τ 2 + τ 2 {\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}

voltadas para baixo (ou seja, no sentido − y {\displaystyle -y} ). Os focos de todas essas parábolas estão localizados na origem.

Fatores de escala bidimensionais

Os fatores de escala para as coordenadas parabólicas ( σ , τ ) {\displaystyle (\sigma ,\tau )} são iguais a

h σ = h τ = σ 2 + τ 2 {\displaystyle h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}

Daí, o elemento infinitesimal de área é

d A = ( σ 2 + τ 2 ) d σ d τ {\displaystyle dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau }

E o laplaciano vale

∇ 2 Φ = 1 σ 2 + τ 2 ( ∂ 2 Φ ∂ σ 2 + ∂ 2 Φ ∂ τ 2 ) {\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)}

Outros operadores diferenciais tais como ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } e ∇ × F {\displaystyle \nabla \times \mathbf {F} } podem ser expressos nas coordenadas (σ, τ) substituindo-se os fatores de escala nas fórmulas gerais para coordenadas ortogonais.

Coordenadas parabólicas tridimensionais

Superfícies coordenadas das coordenadas parabólicas tridimensionais. O parabolóide vermelho corresponde a τ=2, o parabolóide azul corresponde a σ=1, e o semiplano amarelo corresponde a φ =- 60 °. As três superfícies se intersectam no ponto P (mostrado como uma esfera preta) de coordenadas cartesianas aproximadamente iguais a (1,0; -1,732; 1,5).

As coordenadas parabólicas bidimensionais formam a base para dois conjuntos de coordenadas ortogonais tridimensionais. As coordenadas cilíndricas parabólicas são produzidas por projeção na direção z {\displaystyle z} .

A rotação sobre o eixo de simetria das parábolas produz um conjunto de paraboloides confocais, formando um sistema de coordenadas que também é conhecido como "coordenadas parabólicas"

x = σ τ cos ⁡ φ {\displaystyle x=\sigma \tau \cos \varphi }
y = σ τ sin ⁡ φ {\displaystyle y=\sigma \tau \sin \varphi }
z = 1 2 ( τ 2 − σ 2 ) {\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}

onde as parábolas estão alinhadas com o eixo z {\displaystyle z} , sobre o qual a rotação foi realizada. Assim, o ângulo azimutal ϕ {\displaystyle \phi } é definido por


tan ⁡ φ = y x {\displaystyle \tan \varphi ={\frac {y}{x}}}

As superfícies cujo σ {\displaystyle \sigma } é constante formam paraboloides confocais

2 z = x 2 + y 2 σ 2 − σ 2 {\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}

Com concavidade para cima (ou seja, no sentido + z {\displaystyle +z} ), enquanto que as superfícies com τ {\displaystyle \tau } constante formam paraboloides confocais

2 z = − x 2 + y 2 τ 2 + τ 2 {\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}

de concavidade para baixo (ou seja, na direção − z {\displaystyle -z} ). Os focos de todos estes paraboloides estão localizados na origem.

O tensor métrico de Riemann associado a este sistema de coordenadas é

g i j = [ σ 2 + τ 2 0 0 0 σ 2 + τ 2 0 0 0 σ 2 τ 2 ] {\displaystyle g_{ij}={\begin{bmatrix}\sigma ^{2}+\tau ^{2}&0&0\\0&\sigma ^{2}+\tau ^{2}&0\\0&0&\sigma ^{2}\tau ^{2}\end{bmatrix}}}

Fatores de escala tridimensionais

Os três fatores de escala tridimensionais são:

h σ = σ 2 + τ 2 {\displaystyle h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h τ = σ 2 + τ 2 {\displaystyle h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h φ = σ τ {\displaystyle h_{\varphi }=\sigma \tau \,}

Nota-se que os fatores de escala h σ {\displaystyle h_{\sigma }} e h τ {\displaystyle h_{\tau }} são os mesmos do caso bidimensional. O elemento infinitesimal de volume é então

d V = h σ h τ h φ = σ τ ( σ 2 + τ 2 ) d σ d τ d φ {\displaystyle dV=h_{\sigma }h_{\tau }h_{\varphi }=\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\varphi }

E o laplaciano é dado por

∇ 2 Φ = 1 σ 2 + τ 2 [ 1 σ ∂ ∂ σ ( σ ∂ Φ ∂ σ ) + 1 τ ∂ ∂ τ ( τ ∂ Φ ∂ τ ) ] + 1 σ 2 τ 2 ∂ 2 Φ ∂ φ 2 {\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}}

Outros operadores diferenciais tais como ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } e ∇ × F {\displaystyle \nabla \times \mathbf {F} } podem ser expresso nas coordenadas ( σ , τ , ϕ ) {\displaystyle (\sigma ,\tau ,\phi )} substituindo-se os fatores de escala nas fórmulas gerais encontradas em coordenadas ortogonais.

Uma formulação alternativa

A conversão de coordenadas cartesianas para as parabólicas é efetuada através da seguinte transformação:

ξ = x 2 + y 2 + z 2 + z , {\displaystyle \xi ={\sqrt {{\sqrt {x^{2}+y^{2}+z^{2}}}+z}},}
η = x 2 + y 2 + z 2 − z , {\displaystyle \eta ={\sqrt {{\sqrt {x^{2}+y^{2}+z^{2}}}-z}},}
ϕ = arctan ⁡ y x . {\displaystyle \phi =\arctan {y \over x}.}

O jacobiano da transformação de coordenadas dado em termos infinitesimais como sendo

[ d η d ξ d ϕ ] = [ x x 2 + y 2 + z 2 y x 2 + y 2 + z 2 − 1 + z x 2 + y 2 + z 2 x x 2 + y 2 + z 2 y x 2 + y 2 + z 2 1 + z x 2 + y 2 + z 2 − y x 2 + y 2 x x 2 + y 2 0 ] [ d x d y d z ] {\displaystyle {\begin{bmatrix}d\eta \\d\xi \\d\phi \end{bmatrix}}={\begin{bmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}+z^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}+z^{2}}}}&-1+{\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\frac {x}{\sqrt {x^{2}+y^{2}+z^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}+z^{2}}}}&1+{\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{bmatrix}}{\begin{bmatrix}dx\\dy\\dz\end{bmatrix}}}

sob as condições η ≥ 0 , {\displaystyle \eta \geq 0,} e ξ ≥ 0. {\displaystyle \xi \geq 0.}

Se φ = 0, então uma seção transversal é obtida; as coordenadas se limitam ao plano xz:

η = − z + x 2 + z 2 , {\displaystyle \eta =-z+{\sqrt {x^{2}+z^{2}}},}
ξ = z + x 2 + z 2 . {\displaystyle \xi =z+{\sqrt {x^{2}+z^{2}}}.}

Se η=c (uma constante), então

z | η = c = x 2 2 c − c 2 . {\displaystyle \left.z\right|_{\eta =c}={x^{2} \over 2c}-{c \over 2}.}

Esta é uma parábola com foco na origem, para qualquer valor de c. Seu eixo de simetria da parábola é vertical e sua concavidade é voltada para cima.

Se ξ=c então

z | ξ = c = c 2 − x 2 2 c . {\displaystyle \left.z\right|_{\xi =c}={c \over 2}-{x^{2} \over 2c}.}

Esta é uma parábola com foco na origem, para qualquer valor de c. Seu eixo de simetria é vertical e sua concavidade é voltada para baixo.

Agora considere qualquer parábola η=c para cima e qualquer parábola ξ= b para baixo. É desejável encontrar sua interseção:

x 2 2 c − c 2 = b 2 − x 2 2 b , {\displaystyle {x^{2} \over 2c}-{c \over 2}={b \over 2}-{x^{2} \over 2b},}

rearrumando,

x 2 2 c + x 2 2 b = b 2 + c 2 , {\displaystyle {x^{2} \over 2c}+{x^{2} \over 2b}={b \over 2}+{c \over 2},}

evidenciando x²,

x 2 ( b + c 2 b c ) = b + c 2 , {\displaystyle x^{2}\left({b+c \over 2bc}\right)={b+c \over 2},}

cancelando os fatores comuns de ambos os lados,

x 2 = b c , {\displaystyle x^{2}=bc,\,}

tomando a raiz quadrada,

x = b c . {\displaystyle x={\sqrt {bc}}.}


x é a média geométrica de b e c. A abscissa da intersecção foi encontrada. Vamos encontrar a ordenada. Substituindo o valor de x na equação da parábola voltada para cima:

z c = b c 2 c − c 2 = b − c 2 , {\displaystyle z_{c}={bc \over 2c}-{c \over 2}={b-c \over 2},}

em seguida, substituindo o valor de x na equação da parábola voltada para baixo:

z b = b 2 − b c 2 b = b − c 2 . {\displaystyle z_{b}={b \over 2}-{bc \over 2b}={b-c \over 2}.}

zc = zb, com deveria ser. Logo, o ponto de intersecção é

P : ( b c , b − c 2 ) . {\displaystyle P:\left({\sqrt {bc}},{b-c \over 2}\right).}

Desenhe um par de tangentes através do ponto P, cada uma tangente a cada parábola. A reta tangente através do ponto P à parábola superior tem inclinação:

d z c d x = x c = b c c = b c = s c . {\displaystyle {dz_{c} \over dx}={x \over c}={{\sqrt {bc}} \over c}={\sqrt {b \over c}}=s_{c}.}

A reta tangente através do ponto P à parábola inferior tem inclinação:

d z b d x = − x b = − b c b = − c b = s b . {\displaystyle {dz_{b} \over dx}=-{x \over b}={-{\sqrt {bc}} \over b}=-{\sqrt {c \over b}}=s_{b}.}

O produto das duas inclinações é

s c s b = − b c c b = − 1. {\displaystyle s_{c}s_{b}=-{\sqrt {b \over c}}{\sqrt {c \over b}}=-1.}

O produto das inclinações é “uma inclinação negativa”, pois as retas são perpendiculares. Isto é verdade para qualquer par de parábolas com concavidades em direções opostas.

Assim, um par de parábolas intercepta-se em dois pontos, mas quando φ é zero, ele realmente limita as outras coordenadas ξ e η a se moverem no semiplano com x>0, pois x<0 corresponde a φ = π.

Desta forma, um par de coordenadas ξ e η especificam um único ponto no semiplano. Então, fazendo φ entre 0 e 2π, o semiplano gira com o ponto (em torno do eixo z, que é a dobradiça): as parábolas formam paraboloides. Um par de paraboloides opostos formam um círculo, e um valor de φ especifica um semiplano que corta o círculo de intersecção em um único ponto. As coordenadas cartesianas dos pontos são [Menzel, p. 139]:

x = ξ η cos ⁡ ϕ , {\displaystyle x={\sqrt {\xi \eta }}\cos \phi ,}
y = ξ η sin ⁡ ϕ , {\displaystyle y={\sqrt {\xi \eta }}\sin \phi ,}
z = 1 2 ( ξ − η ) . {\displaystyle z={\begin{matrix}{\frac {1}{2}}\end{matrix}}(\xi -\eta ).}
| d x d y d z | = | 1 2 ξ η cos ⁡ ϕ 1 2 η ξ cos ⁡ ϕ − ξ η sin ⁡ ϕ 1 2 ξ η sin ⁡ ϕ 1 2 η ξ sin ⁡ ϕ ξ η cos ⁡ ϕ − 1 2 1 2 0 | ⋅ | d η d ξ d ϕ | {\displaystyle {\begin{vmatrix}dx\\dy\\dz\end{vmatrix}}={\begin{vmatrix}{\frac {1}{2}}{\sqrt {\frac {\xi }{\eta }}}\cos \phi &{\frac {1}{2}}{\sqrt {\frac {\eta }{\xi }}}\cos \phi &-{\sqrt {\xi \eta }}\sin \phi \\{\frac {1}{2}}{\sqrt {\frac {\xi }{\eta }}}\sin \phi &{\frac {1}{2}}{\sqrt {\frac {\eta }{\xi }}}\sin \phi &{\sqrt {\xi \eta }}\cos \phi \\-{\frac {1}{2}}&{\frac {1}{2}}&0\end{vmatrix}}\cdot {\begin{vmatrix}d\eta \\d\xi \\d\phi \end{vmatrix}}}

Ver também

  • Coordenadas ortogonais
  • Sistemas de coordenadas ortogonais bidimensionais:
  • Sistemas de coordenadas ortogonais tridimensionais:

Referências

  • Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Parabolic coordinates», especificamente desta versão.
  • Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 660 páginas. ISBN [[Special:BookSources/0-07-043316-X, LCCN 52-11515|0-07-043316-X, <span class="noprint">[[Library of Congress Control Number|LCCN]]&nbsp;[http://lccn.loc.gov/52011515 52-11515]</span>]] Verifique |isbn= (ajuda) 
  • Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 185–186. LCCN 55-10911 
  • Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 180 páginas. LCCN 59-14456, ASIN B0000CKZX7 
  • Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 96 páginas. LCCN 67-25285 
  • Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. 114 páginas. ISBN 0-86720-293-9  Same as Morse & Feshbach (1953), substituting uk for ξk.
  • Moon P, Spencer DE (1988). «Parabolic Coordinates (μ, ν, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd, 3rd print ed. New York: Springer-Verlag. pp. 34–36 (Table 1.08). ISBN 978-0387184302 

Ligações externas

  • Descrição em MathWorld das coordenadas parabólicas – inglês