Alpha-stabile Verteilungen

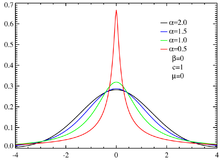
Die Familie der α-stabilen Verteilungen ist eine Verteilungsklasse von stetigen Wahrscheinlichkeitsverteilungen aus der Stochastik, die durch folgende definierende Eigenschaft beschrieben werden: sind ${\displaystyle X_{1},X_{2},\dotsc ,X_{n},X}$ unabhängige, identisch verteilte Zufallsvariablen, und gilt für die Summe

${\displaystyle X_{1}+X_{2}+\dotsb +X_{n}\sim c_{n}X}$ für alle ${\displaystyle n\in \mathbb {N} }$ und eine Folge ${\displaystyle (c_{n})_{n\in \mathbb {N} }}$,

so nennt man ${\displaystyle X}$ stabil verteilt, wobei ${\displaystyle \sim }$ als „hat dieselbe Verteilung wie“ zu lesen ist. Man kann zeigen, dass die einzig mögliche Wahl ${\displaystyle c_{n}=n^{1/\alpha },\alpha \in (0,2]}$ ist. Die reelle Zahl ${\displaystyle \alpha }$ nennt man hierbei den Formparameter. Da die Theorie der stabilen Verteilungen maßgeblich durch Paul Lévy mitgestaltet wurde, nennt man jene Verteilungen deshalb auch manchmal Lévy-stabile Verteilungen.

Beispiele

Obwohl die stabilen Verteilungen für jedes ${\displaystyle \alpha }$ des obigen Intervalls wohldefiniert sind, ist nur für wenige spezielle Werte von α die Dichte explizit gegeben:

• Die Normalverteilung mit Erwartungswert 0 ist stabil mit Formparameter ${\displaystyle \alpha =2}$, denn bekanntlich gilt

${\displaystyle X_{1},X_{2},\ldots ,X_{n}\sim {\mathcal {N}}(0,\sigma ^{2})\Rightarrow \sum _{i=1}^{n}X_{i}\sim {\mathcal {N}}(0,n\sigma ^{2})\sim n^{1/2}{\mathcal {N}}(0,\sigma ^{2})}$. Die Normalverteilung ist die einzige Verteilung mit dem Formparameter ${\displaystyle \alpha =2}$.

• Die zentrierte Cauchy-Verteilung erfüllt die Gleichung

${\displaystyle X_{1},X_{2},\ldots ,X_{n}\sim {\rm {Cauchy}}(0,a)\Rightarrow \sum _{i=1}^{n}X_{i}\sim n\,{\rm {Cauchy}}(0,a)}$

sie ist also stabil mit Formparameter ${\displaystyle \alpha =1}$.

• Die (eigentliche) Standard-Lévy-Verteilung ist stabil mit ${\displaystyle \alpha ={\frac {1}{2}}}$.

Eigenschaften

• Die charakteristische Funktion einer α-stabilen Verteilung ist durch

${\displaystyle \psi _{\alpha ,\beta ,c,\mu }(t)={\begin{cases}\exp \left(i\mu t-c|t|^{\alpha }\left(1-i\beta \tan \left({\frac {\pi \alpha }{2}}\right)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha \in (0,1)\cup (1,2]\\\exp \left(i\mu t-c|t|\left(1+i\beta {\frac {2}{\pi }}\ln(|t|)\operatorname {sgn}(t)\right)\right)&{\text{für }}\alpha =1\end{cases}}}$

gegeben^[1][2] Der Parameter ${\displaystyle \alpha \in (0,2]}$ heißt charakteristischer Exponent. Der Parameter ${\displaystyle \beta \in [-1,1]}$ heißt Schiefeparameter. Der Parameter ${\displaystyle c}$ ist positiv. Der Parameter ${\displaystyle \mu \in \mathbb {R} }$ ist ein Lageparameter.

• Endliche Varianz existiert nur für ${\displaystyle \alpha =2}$. Dies folgt unmittelbar aus dem zentralen Grenzwertsatz. Für ${\displaystyle \alpha =2}$ spezialisiert sich die charakteristische Funktion zu ${\displaystyle \exp(i\mu t-ct^{2})}$; dies ist charakteristische Funktion einer Normalverteilung mit dem Erwartungswert ${\displaystyle \mu }$ und der Varianz ${\displaystyle 2c}$.
• Für ${\displaystyle 1<\alpha \leq 2}$ hat die Verteilung den Erwartungswert ${\displaystyle \mu }$, für ${\displaystyle \alpha \leq 1}$ existiert kein Erwartungswert. Dies folgt mit dem Gesetz der großen Zahlen.
• Alle α-stabilen Verteilungen sind unendlich teilbar und selbstähnlich („selfdecomposable“).

Analoge Konzepte für diskrete Verteilungen

Für diskrete Verteilungen gibt es den Begriff der diskret-stabilen Verteilung^[3][4], ein Beispiel einer solchen Verteilung ist die Poisson-Verteilung, welche bei diskret-stabilen Verteilungen einen ähnlichen Stellenwert einnimmt, wie die Normalverteilung bei Lévy-stabilen kontinuierlichen Dichten^[5].

Literatur

• Achim Klenke: Wahrscheinlichkeitstheorie. 2. Auflage. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76317-8, Kap. 16.

Einzelnachweise

1. ↑ Paul Embrechts, Thomas Mikosch, Claudia Klüppelberg: Modelling extremal events (= Stochastic Modelling and Applied Probability. Band 33). Springer-Verlag, Berlin / Heidelberg / New York 1997, ISBN 3-540-60931-8, Theorem 2.2.3, S. 71, doi:10.1007/978-3-642-33483-2. 
2. ↑ Rick Durrett: Probability: Theory and Examples. 4. Auflage. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76539-8, S. 141.
3. ↑ F. W. Steutel, K. van Harn: Discrete analogues of self-decomposability and stability. In: The Annals of Probability. Band 7, Nr. 3, S. 893–899, doi:10.1214/aop/1176994950. 
4. ↑ Luc Devroye: A triptych of discrete distributions related to the stable law. In: Statistics and Probability Letters. Band 18, Nr. 5, S. 349–351, doi:10.1016/0167-7152(93)90027-G. 
5. ↑ Stochastic Population Processes Analysis, Approximations, Simulations, Eric Renshaw, 2015, ISBN 9780191060397, Seite 134, https://books.google.de/books?id=pqE1CgAAQBAJ&pg=PA134